|
1927 年九月,在义大利科摩(Como)召开了一次纪念义大利科学家 Alexaudro Volta(1745-1827) 逝世一百周年会议,许多世界知名科学家应邀参加.Niels Bohr 在会议中首度公开地演讲他的互补原理(complementary principle). Bohr 采用了大量的哲学语言来阐释互补原理,使大家感到震惊与困惑!
当时大多数人对于测不准关系及互补原理的深刻内涵还不大明了. 事后法国物理学家 Eugene Wigner 言道,Bohr 的演讲不会使我们当中任何一位改变对量子力学的看法.
几个星期后在布鲁塞尔举行的第五届 Solvay Congress,包括 Bohr, Einstein, Max Born, Ervin Schrodinger, Louis deBroglie, Werner K. Heisenberg 等世界最著名的科学家都出席了这项盛会. Bohr 在会议中重述了他在科摩会议上的观点.由于 Einstein 并未参加科摩会议, 这还是他首次听到 Bohr 亲自阐述互补原理和对量子力学的诠释.Einstein 一直对量子力学的机率解释感到不满, 他曾在写给 Born 的信中提到: 「量子力学虽然令人赞叹,但在我的心中有个声音告诉我, 它还不是那真实的东西……我无论如何不相信上帝会在掷骰子!」因此人们急切地想知道 Einstein 对 Bohr 观点的反应.本世纪最伟大的两位科学巨人之间的大战就此揭开序幕.
Einstein 起来发言,表示赞同量子力学的系综(ensemble)机率解释. deBrodlie-Schrodinger 波不是代表单个粒子,而是代表分布在空间中的一个粒子系综. 理论所提供的信息是关于这个过程的系综的,因此不赞成量子力学是描述单一过程的完备理论.
Einstein 的发言立即激起了与会学者的热烈讨论.虽然 Einstein 和 Bohr 两人都尽量地使用客气的言词和有礼的态度,尊重自己的对手.但两人一交锋,就充分显示出问题的尖锐性.
Bohr 极力地想说服 Einstein:难道不就是你第一个突破古典物理的框架,提出相对论和光的量子理论吗? 难道不就是你首先在 1905 年提出光的波粒二象性思想的吗?不就是你将机率的概念引入来解释辐射问题的吗? 像你这样一个量子物理的开拓者,难道不应该进一步接受更新的量子力学观点, 把理论更进一步向前推进?
然而 Einstein 并不听这一套.他坚信,有一个离开知觉主体而独立存在的客观世界, 是一切自然科学的基础.为 Einstein 立传的作家 A.Pais 回忆道: 「有一次和 Einstein 同行,他突然停下来,转身问我是否真的相信, 月亮只有在我去看它的时候才存在?」
Einstein 企图用一些理想实验来反驳测不准原理.首先,他设计了一个让电子通过单狭缝绕射的实验, 认为这个实验可以提供一个精确的时空坐标,同时又能提供对此过程中能量和动量交换平衡的详细说明.
然而,Bohr 很决的指出,他不能避免在测量时仪器对电子的干扰,即电子与狭缝边缘的相互作用. 这在分析理想实验是十分重要的. Einstein 见单狭缝难不倒 Bohr,第二天又想出了新的实验.他承认用确定位置坐标的同一系统来精确测量动量是不可能的, 所以他以分开的装置,一个测位置,一个测动量.他设计了一个电子通过双狭缝干涉的实验, 当双狭缝开启时,从屏幕出现的亮点可以知道电子垂直方向的动量,分别关上其中一个狭缝, 就可以知道电子的确实位置. 然而 Bohr 在仔细思考后发现,如果关上其中任何一个狭缝,实验的状态就完全改变了. 当双狭缝开启时,即便电子一个个发射出来,最后仍会在屏上形成干涉条纹.假如轮流开启一个狭缝, 虽然可以得知电子究竟经过那个狭缝,但最后却不会再有干涉条纹了.就这样,这个本来是 Einstein 用来反驳量子力学的理想实验,经由 Bohr 的解释在今日已成了说明测不准关系和互补原理的标准范例.
据 Heisenberg 事后回忆,Einstein 往往在吃早饭的时候告诉 Bohr 他所想出来反驳测不准原理的理想实验.Bohr 立即著手分析,总是在吃晚饭前, Bohr 告诉 Einstein,他的实验是驳不倒测不准原理的.如此接连数日, 甚至使一些原本怀疑 Copenhagen 解释的科学家,都转而支持 Bohr 的立场了. 会议落幕了.虽然 Bohr 成功的捍卫了测不准原理和互补性诠释的无矛盾性, 但 Einstein 并未服输.他坚持:「上帝并不掷骰子.」这场大战正如火如荼地展开呢!
|
Einstein 光盒 |
|
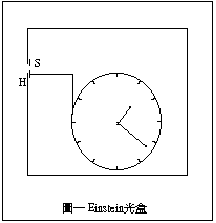
三年后,第六届的 Solvay Congress 开幕了.各国科学家都热烈地期待著 Einstein 和 Bohr 之间新的论战.这次 Einstein 经过了三年的深思熟虑,显得胸有成竹. 他在黑板上画了一个盒子,盒上有一个小孔 H,H 可由快门 S 来启闭. 快门则由盒中的时钟机械置来控制,小盒的重量是可以测量的.盒中装有一些辐射物质. 我们可以调节快门使得刚好放出一个粒子之后就关闭(见图一). 透过时钟,可以精确的量出粒子放出的时间.另外,测量粒子放出后盒子的重量, 我们也可以知道粒子的质量.经由 E=mc2 的关系式,能量也可以准确地计算出来. 于是违反了
>E>t≠h/2 π
的测不准关系.这就是著名的 Einstein 光盒(Einstein's box)实验.
由于实验根本不涉及观测仪器的问题,根本没有外来粒子会改变粒子的运动. 所以测不准关系破灭了,因果律和准确性都恢复了.一场新的论战剧性的展开了.
这会儿 Bohr 遇到了严重的挑战,无法马上找到问题的答案.他喃喃地说,如果 Einstein 是对的,那物理学就完了.他和他的同事一夜未眠,检查实验的每一个细节,想要找出 Einstein 到底错在那里. 经过通宵的奋战之后,Bohr 终于找出了反驳 Einstein 的办法.
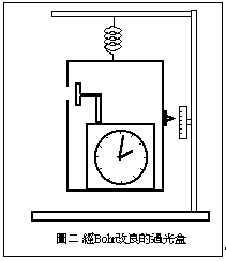 第二天,Bohr 也在黑板上画了一个草图(见图二).但和 Einstein 不同的是,他给出量称小盒重量的方法. 他用弹簧把小盒吊起来.盒上有一指针,可以沿固定在支架上的标尺移动. 这样就可以读出小盒在粒子跑出前后的重量了.Bohr 请大家回忆 Einstein 的广义相对论中的等效原理. 当时钟在重力场中发生位移时,它的快慢会发生变化.当粒子跑出盒子而导致盒子重量变化时, 盒子将在重力场中移动一段距离.这样子读出的时间也会有所改变,因而导出测不准关系. 这是广义相对论中著名的红位移公式: 第二天,Bohr 也在黑板上画了一个草图(见图二).但和 Einstein 不同的是,他给出量称小盒重量的方法. 他用弹簧把小盒吊起来.盒上有一指针,可以沿固定在支架上的标尺移动. 这样就可以读出小盒在粒子跑出前后的重量了.Bohr 请大家回忆 Einstein 的广义相对论中的等效原理. 当时钟在重力场中发生位移时,它的快慢会发生变化.当粒子跑出盒子而导致盒子重量变化时, 盒子将在重力场中移动一段距离.这样子读出的时间也会有所改变,因而导出测不准关系. 这是广义相对论中著名的红位移公式:
>T=T△φ/c2?
公式表示一个在重力场中移动的时钟,在移过一个位势差 △φ 时在时间 T 内时钟快慢的改变. Bohr随即用红位移公式导出了测不准关系.
这下子 Einstein 不得不承认 Bohr 的推论是无懈可击的! 他自己在设计这个理想实验的时候, 居然没有考虑到广义相对论的效应,实为一大疏忽,真是遗憾! Bohr 用 Einstein 的相对论驳倒了他本人,取得了第二回合的胜利.
Bohr 的胜利获得了大多数物理学家的赞同.Copenhagen 解释也被奉为是量子力学的正统解释. Einstein 对他的失败欣然接受.还有什么东西比他自己的理论对他更有说服力呢? 这次论战的结果是 Einstein 对量子力学态度的一个转捩点. 他意识到在量子力学的形式体系内是驳不倒测不准原理的.他不再怀疑测不准原理了. 但他仍然对 Copenhagen 的诠释持否定的观点.因为量子力学本身不能证明机率特性是微观粒子本身的属性. Einstein 失败了,但是并没有被说服.相反的,由于 Einstein 坚持他的信念, 而把论战提升到更高的境界.并在物理学及哲学上产生许多新的问题.
主要取材自:探幽入微之路--量子历程
|
EPR 反论 |
|
1935 年 5 月, 在 Physical Review 上 Einstein 和他的两位同事 B. Podolsky和 N. Rosen 共同发表了一篇名为 「Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?」 (能认为量子力学对物理世界的描述是完备的吗?) 三个人异口同声地回答:「不!」
在这篇著名的文章中,作者首先阐述了他们对物理理论的看法: 一个严谨的物理理论应该要区别「客观实体」(object reality) 以及这个理论运作的观点. 客观实体应独立于理论而存在.在判断一个理论是否成功时,我们会问自己两个问题:
(1)这个理论是否正确?
(2)理论的描述是否完备?
只有当这两个问题的答案是肯定时,这样的理论才是令人满意的.理论的正确性当由实验来决定. 而关于量子力学的描述是否完备则是这篇文章探讨的主题. 在进一步讨论理论的完备性之前,我们必须先定义什么是完备性.作者们提出了一项判别完备性的条件: 每一个物理实体的要素必须在理论中有一对应物(every element of the physical reality must have a counterpart in the physical theory) 因此我们决定了什么是「物理实体的要素」,那么第二个问题就容易回答了.
那么,究竟什么是「物理实体的要素」呢? 作者们以为: 「如果,在不以任何方式干扰系统的情况下, 我们能准确地预测(即机率为一)某一物理量的值,那么必定存在一个物理实体的要素与这个物理量对应.」 他们认为,只要不把这个准则视为一必要条件,而看成是一充分的条件, 那么这个判别准则同样适用于古典物理以及量子力学中对实在的概念.
举例来说,在一维系统中,一个以波函数
φ(x) = exp(ip0x/2πh)
(其中 p0 是一常数,i 表纯虚数,h 为 Planck 常数)描述的粒子.其动量的算符为
h d
p = ---- ----
2πi dx
因此,
pφ(x) = p0φ(x)
所以动量有一确定的值 p0. 因此在这种情形下动量是一物理实体.反之,对位置算符 q 而言, qφ = xφ ≠ aφ
对任何实数 a 而言
因此粒子的位置并没有一确定的值.它是不可预测的,仅能以实验测定之. 然而任何一实验的测定都将干扰到粒子而改变其状态,被测后的粒子将再也不具动量 p0 了. 对于此情况,我们说当一粒子的动量确定时,它的位置并非一物理实体.
一般来说在量子力学中,对两个不可对易的可观察量(observable)而言, 知道其中一个物理量的准确知识将排除对另外一个的准确知识. 任何企图决定后者的实验都将改变系统的状态而破坏了对前者的知识. 至此,作者们发现我们面临了如下的两难局面:
(1)或者,在量子力学中波函数对物理实在的描述是不完备的.
(2)或者,两个对应于不可对易算符的物理量不能同时是实在的(即具有确定的值).
因为,若两个不可对易的物理量同时具有确定的值,根据作者们对完备性的条件, 在波函数的描述中应包含这些值.但事实上并非如此,因此波函数的描述是不完备的.
在量子力学中,通常假设了波函数包含了描述物理系统一切完备的资讯.乍看之下, 这样的假设似乎很合理.然而,Einstein 等人指出,在这个假设之下, 配合他们对物理实体的判别准则,将导出 (2) 也是错的.因此这是一个矛盾.
这就是著名的 EPR 反论(EPR paradox 或 EPR dilemma).
Einstein 等设计了一个理想实验来证实他们的观点.假设现在有两个粒子在 t=0 到 t=T 的时间之内相互作用,但在 t>T 之后分开,不再有任何交互作用.根据 Schrodinger 方程式,我们仍然可以算出以后任何时刻两个粒子的状态.现在, 注意到两个粒子动量和算符 p1+p2 及位置差算符 x1-x2 是可对易的. 因此可以同时具有确定的值,即有共同的本徵态(eigenstate). 例如
φ(x1,x2) = δ(x1-x2-a)
δ 是 Dirac 的 delta 函数.这代表了动量和为零以及位置差为 a 的本徵态. 现在假如我们去测量粒子 1 的位置,而得到结果 x1,那么,我们可以同时地肯定粒子 2 的位置必定是 x1-a. 换言之,在不扰动粒子 2 的情形之下我们便可确定粒子 2 的位置. 因此,根据 EPR 的判别准则,粒子 2 的位置是实在的.同样的,若是我们去测量粒子 1 的动量而得到结果 p,我们也能肯定粒子 2 具有动量 -p. 因此粒子 2 的动量也是实在的. 由于两个粒子已经足够地分开,而没有任何交互作用,粒子 2 不可能知道我们究竟要测量粒子 1 的位置还是动量,从而「决定」它要在位置 x1-a 或具有动量 -p,这两个量必定是同时存在的(即使我们不能同时去量它们). 换言之,就是违反了前面 (2) 的条件.
在假设 (1) 错的情形之下,Einstein 等推出了 (2) 也是错的结论,而这是不可能的. 因此 (1) 一定是对的.所以 Einstein 等大胆的宣布,量子力学的描述必是不完备的. 在获得了这样的结论之后,Einstein 等同时期待了一个新而完备的理论将会出现. 纵观 Einstein 的论证,我们发现他们的推论中隐含了两项假设:
(1)物理实在是独立于观测者而客观地存在的.
(2)两粒子间传递讯息的速度不能超过光速,不存在超距作用(action-at-a-distance). 这项假设后来被称为 Einstein 定域性原理(locality principle).
当 EPR 的论文发表之后,立刻引起了广大的回响,甚至成了新闻焦点. 当时的纽约时报以头条报导此事:「Einstein 抨击量子理论」 |
|
Bohr 的反击 |
|
EPR 的抨击再度激起了两位巨人之间新的论战.据当时 Bohr 的同事 Leon Rosenfeld 回忆道: 「这对我们来说简直是晴天霹雳! (onslaught that came down upon us like a bolt from the blue.) 对 Bohr 的影响太大了...」, 「当 Bohr 听到我报告 Einstein 的论证后,马上放下所有的工作说,我们要立刻澄清这个误解!」
同年十月,Bohr 也在 Physical Review 上发表了一篇同名的论文,反驳 Einstein 等人的观点.Bohr 首先批评了 EPR 对物理实体的判别准则.Bohr 以为一个物理量只有在当它被测量之后才是实在的.在 EPR 的理想实验中, 虽然我们对粒子的测量的确会得到预期的结果,然而只有在我们安排此一实验测量之后, 该物理量(位置或动量)才是实在的.所以 EPR 的判别准则是有问题的.
其次 Bohr 分析了 EPR 的理想实验,认为两个粒子在分开之后, 仍然存在著某种关联性.因此在对粒子 1 做测量时,仍应视为对整个系统的扰动. 换言之,Bohr 并不赞同 Einstein 的定域性原理.
量子力学是一个和谐的数学形式体系.它的预测与微观领域的实验结果都符合得很好. 既然一个物理理论的预测都能够被实验所证实,而且实验又不能得出比理论更多的东西, 那么,我们还有什么理由对这个理论提出更高的「完备性」要求呢? 量子力学确实描述了微观客体对巨观仪器的度量表现,这种巨观度量只能得出微观客体运动的统计结果. 量子力学也只能透过这些巨观表现去猜测微观客体的某些属性,它确实反映了以作用量子为下限的客体之运动状况. 因此,从它自身逻辑的相容性与和经验符合的程度来看,Bohr 认为,量子力学是完备的.
不过 Bohr 的这篇文章里,充满了许多艰深的言词和哲学性的思想,使人不易抓住作者的中心思想. 尤其是 Bohr 以为一个物理量只有当它被测量了以后才是实在的.这样的观点, 使人不禁想问:「难道月亮只有我去看她时才存在吗?」 |
|
Bohm 的理想实验 |
|
1951 年,Princeton 大学教授 David Bohm 提出了一个新的版本的 EPR 反论.
Bohm 的方案是考虑一对处在单态(singlet state)的自旋 1/2 粒子. 意即,粒子的自旋态为:(这里读者可能需要一点量子力学自旋及角动量相加理论的基础...)
|spin singlet> = (|z+>|z-> - |z->|z+>)/√2
两个粒子互相分开,并分别进入一侦测器 A, B, 如下图所示:
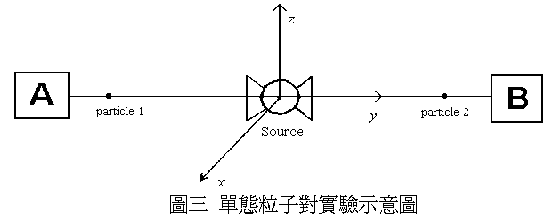
| B | +---+ particle 1 source particle 2 +---+ -->
侦测器 A,B 是一 Stern-Gerlach 装置,可以安排成测量粒子任一方向自旋角动量的分量. 现在假设 A 被安排成测量粒子 1 的 z 轴自旋分量 Sz, B 也被安排成测量粒子 2 的 z 轴自旋分量.由于粒子对处于 singlet state, 我们不知实验结果为何, 只知道获得正负 h/2 的机率都是百分之五十.然而,若是 A 测量的结果是 +h/2, 那么我们可以确定 B 的结果必是 -h/2.
这种情形有点儿像在袋子中放了黑白两球,我们伸手去拿一球,那拿到黑球或白球的机率各是 50%. 但假如我们拿到了白球,那袋中剩下的球必是黑球!
然而这样的类比还是太过简单了.量子系统可比这复杂多了! 因为我们也可以安排 A,B 去测量自旋的 x 轴分量或是其它方向的分量.我们的量子球不但可以是黑和白的,也可以是红和绿的!
一个自旋 1/2 粒子的 Sx 及 Sz 的本徵态有下面的关系:
|x+> = (|z+> + |z->)/√2
|x-> = (|z+> - |z->)/√2
|z+> = (|x+> + |x->)/√2
|z-> = (|x+> - |x->)/√2
因此若将 singlet state 用 |x+> 和 |x-> 表示,则为
|singlet state> = (|x->|x+> - |x+>|x->)/√2
所以同样地,如果我们量测粒子 1 自旋的 x 轴分量,得到的结果为正,那量测粒子 2 自旋的 x 轴分量结果必为负.(这并不奇怪,因为 singlet state 的自旋总角动量为零, 因此两个粒子在任一方向的自旋分量必相反.)
现假设,让 A 量测粒子 1 的 Sx, 而 B 量测粒子 2 的 Sz, 那么即使我们得到 A 的结果为正,我们仍不知道 B 的结果为何.因为虽然我们知道粒子 2 的 Sx, 它的 Sz 仍然完全未定.我们得到的结果仍是正负各百分之五十.
根据以上讨论,我们有下面的结果:
(1)如果 A 和 B 同时量测 Sz, 那么两者的测量结果有百分之百的相关程度(即符号完全相反)
(2)如果 A 量 Sx 而 B 量 Sz, 那么两者的结果将没有任何的相关.
看来,在 B 处测量的结果将和 A 处做何种量测有关.但是 A,B 可以相距几公尺, 几公里,甚至几光年(原则上)! 在 B 处的粒子 2 如何能「知道」我们将在 A 处做什么测量,进而「决定」它的行动呢? (若测同一轴就跳到和 A 相反的方向, 若测相互垂直的方向就可以随机?)
所以,在认为没有超距作用,即在 A 处的量测不可能影响在远方的粒子 2 的情形之下,我们只好认为,两个粒子在出发之时,就已经「想」好了要「告诉」 侦测器何种结果.而且,两个粒子的「想法」是刚好相反的.如下图所示:

· | B | +---+ ↑ ↑ +---+ z+, x-, y-,... z-,x+,y+,... -->
因此,两个不可对易的算符 Sx 和 Sz 将同时地具有「物理实在」(physical reality). 或者,我们可以把它叫做「密码」或「指令集」更恰当.
我们可以将粒子的「思想」称为是「密码」或「指令集」.粒子也许并非想像中的无知, 到了侦测器前面,才临时地「掷骰子」决定自己命运.冥冥之中正有一股力量在操纵一切:一种隐藏的, 未知的参数控制了粒子的行为.这种「隐藏」的性质决定了我们观察的结果(spin up, spin down). 我们所见到的机率现象,只是统计的,平均的结果.这种观点称为「隐变量理论」(Hidden-variable theory)或是量子力学的「隐变量解释」.其实这样的观点并不陌生.例如在热力学中气体的温度, 压力等巨观物理量,都可以用分子运动论,以大量分子作无规律热运动的统计平均效果加以说明. 因此分子的质量,速度等可以看成是热力学中的「隐变量」,而分子运动论就是热力学的「隐变量解释」. 然而,量子力学的隐变量理论将会遭遇严重的困难.详见后述.
粒子的密码或指令集就是 EPR 所谓的「物理实体(physical reality)」. 然而这些实体是分别属于两个不对易算符 Sx 和 Sz 的.
量子力学对自旋的描述(二维的 Hilbert 空间)显然不能(同时)包含这些实体, 它们在理论中没有对应物.因此,不能认为量子力学的描述是完备的.
到此为止,我们可以根据 Einstein 和 Bohm 的理想实验,将 EPR 的推论过程总结如下:
Einstein 定域性原则,无超距作用.
==>两个不可对易的物理量(如 p 及 x, Sx 及 Sz 等)将同时具有确定的值.
==>这些值并未包含在波函数(或自旋态等)的描述中.
==>量子力学的描述是不完备的.
可以看出争论的焦点在于定域性原则上.只要承认这个原则,似乎不可避免会得到 EPR 的结论.
然而,只要在微观的尺度上,量子力学能提出符合实验的完善描述,并作有效的预测, 我们还能苛求什么呢?
「大自然就是这个样子!」我们应该安心地运用量子力学的思想于研究工作上, 何必去管什么基础问题呢? 量子力学的描述完不完备? 管它的呢!
事情至此似乎已变成纯是哲学观点的争论了.然而,到了 1965 年,EPR 反论发表 30 年之后,情况有了戏剧性的转变. |
|
Bell 定理 |
|
1964 年,J.S.Bell 在 Physics I 上发表了一篇论文,指出任何企图保持 Einstein 定域性原则的隐变量理论都将不能和量子力学相容.这是著名的 Bell 定理.Bell 利用 Bohm 的单态粒子对实验推导了一个不等式, 说明了定域性隐变量理论的相关性(correlation)和量子力学是不同的.
假设如同前面 Bohm 的实验装置,A, B 侦测器可以被安排成测量 a, b, c 三个不同方向的自旋分量.a, b, c 三个方向是任意的,不需要互相垂直, 甚至可以在同一个平面上. 如果,粒子从发射器出发之时已带有某种「密码」(这是定域性隐变量理论所预期的), 如 (a+,b+,c-), 代表了粒子进入 a 方向的侦测器结果将是正的, b 方向结果也是正,而 c 方向结果为负.由于两个粒子自旋方向相反, 这样的组合共有八种,如下所示:
粒子 1 粒子 2
N1 (a+,b+,c+)(a-,b-,c-)
N2 (a+,b+,c-)(a-,b-,c+)
N3 (a+,b-,c+)(a-,b+,c-)
N4 (a-,b+,c+)(a+,b-,c-)
N5 (a+,b-,c-)(a-,b+,c+)
N6 (a-.b+.c-)(a+,b-,c+)
N7 (a-,b-,c+)(a+,b+,c-)
N8 (a-,b-,c-)(a+,b+,c+)
重复这样的实验 N 次,设各种情况出现次数分别是 N1, N2,... N8. 自然的, N1+N2+......+N8 = N.
令 P(a+,b+) 表示 A 侦测器在 a 方向测得结果为正,B 侦测器在 b 方向测得结果为正的机率.而 P(b+,c-) 表示 A 侦测器在 b 方向测得正,B 侦测器在 c 方向测得负的机率,等等.例如,P(a+,b+) = (N3+N5)/N, P(b+,c-) = (N1+N4)/N.
现定义 a, b 方向的相关程度系数 E(a,b) 为
E(a,b) = P(a+,b+) + P(a-,b-) - P(a+,b-) - P(a-,b+)
注意到 E(a,b) = E(b,a). 它代表了 A, B 侦测器在 a, b 两方向测量结果的相关程度.例如,在 a=b 时,P(a+,b+) = P(a-,b-) = 0, 而 P(a+,b-) = P(a-,b+) = 1/2, 因此 E(a,a) = -1. 这表示说若 A, B 侦测器被安排成测同方向的自旋分量,所得结果必定相反.又如,a=-b, E(a,-a) = 1, 即 A, B 的结果必相同. 如果 a 和 b 相互垂直,则 P(a+,b+) = P(a-,b-) = P(a+,b-) = P(a-,b+) = 1/4, 所以 E(a,b) = 0. 这是说如果两侦测器所测的方向互相垂直,则两者的结果没有任何相关. 由此可见这个定义符合我们对「相关」的直觉含义.
根据定义,我们有
E(a,b) = (N3+N5+N4+N6-N1-N2-N7-N8)/N
同理
E(a,c) = (N2+N5+N4+N7-N1-N3-N6-N8)/N
E(c,b) = (N3+N7+N2+N6-N1-N4-N5-N8)/N
现在因为 Ni (1≤i≤8) 都是大于等于零的整数,因此
2(N3+N6-N2-N7) ≤ 2(N3+N6+N2+N7)
两边加上 N1+N4+N5+N8, 得
2(N3+N6-N2-N7)+N1+N4+N5+N8 ≤ N3+N6+N2+N7+N
同除以 N, 得
2(N3+N6-N2-N7)/N ≤ (N3+N7+N2+N6-N1-N4-N5-N8)/N + 1
我们发现不等式右边即是 E(c,b) + 1, 而左边是
E(a,b) - E(a,c) = 2(N3+N6-N2-N7)/N
同理,
-E(c,b) - 1 ≤ E(a,b) - E(a,c)
因此
|E(a,b) - E(a,c)| ≤ 1 + E(c,b)
这就是著名的 Bell 不等式.这对任意方向的 a, b, c 而言都成立.
现在,让我们来看看 Bell 不等式和量子力学的预测是否相符. 我们要以量子力学的方法去计算 P(a+,b+), P(a+,c+) 以及 P(c+,b+). 令 S.a, S.b, S.c 的本徵态分别是 |a+>,|a->, |b+>,|b-> 和 |c+>,|c->. 例如,要计算 P(a+,b+), 我们假设粒子 1 进入 a 方向的侦测器得到结果为正(这机率显然是1/2). 因此,粒子 2 必将处于 |a-> 的状态.在 B 处我们测量粒子 2 的 b 方向自旋分量. 按量子力学,我们必须将 |a-> 按 |b+> 和 |b-> 展开.
如果 a, b 两方向的夹角是 θab, 那么结果是(up to a phase constant)
|a-> = sin(β/2 )exp(-iα/2)|b+> - cos(β/2)exp(iα/2)|b->
其中 α, β, γ=0 是 Euler 角(把 b 放在 z 轴上), β = θab. 如图五所示.

所以,粒子进入 b 方向侦测器得到结果是正的机率是
sin2(θab/2)
因此
P(a+,b+) = sin2(θab/2)/2
同样的
P(a-,b-) = sin2(θab/2)/2
以及
P(a+,b-) = P(a-,b+) = cos2(θab/2)/2
所以
E(a,b) = sin2(θab/2) - cos2(θab/2) = -cosθab = -a.b
同理 E(a,c) = -cosθac,
E(c,b) = -cosθcb
根据 Bell 不等式,我们得到
|cosθac - cosθab| ≤ 1 - cosθcb
对任意的 a, b, c 皆成立.
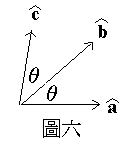
然而,我们发现这是不可能的.例如,让 a, b, c 在同一平面上,而且 b 就在 a,c 的角平分线上,如图六所示. θab = 2θ,θab = θcb = θ,于是
cos2θ - 2cosθ + 1 ≥ 0 或 cos2θ ≥ cosθ
当 0 < θ < π/2 时,显然是不可能的.
J.F.Clauser 及 M.A.Horne 等于 1969 年改进并推广了 Bell 不等式. 他们的方案是利用光子对的偏振(polarization)相关性.Clauser 等并提出了可行的实验,检验 Bell 不等式. 其它如 E.P.Wigner, A.Shimony, H.P.Stapp 等人也都相继提出了类似的不等式. 由于 Bell 不等式完全基于 Einstein 的定域性原理,因此 Bell 定理提供了检验定域性原理的一项利器.如果实验结果证实 Bell 不等式是对的, 那么就违反了量子力学的预测;相反的,如果实验结果违背了 Bell 不等式,也就同时否定了 Bell 不等式的前提,Einstein 定域性原理.
终于,这场论战又从哲学回到了物理,等待实验来判定谁胜谁败. |
|
实验结果 |
|
70 年代起,有一连串的实验开始检验 Bell 不等式.其中包括了级联光子对 (cascade-photon)相关实验,正负电子对湮灭(positronium annihilation)的高能相关γ光子实验, 以及质子对散射(proton-proton scattering)实验等,大部分的实验都显示了违背 Bell 不等式的结果! 利用正负电子对湮灭的实验,有
吴健雄, L.R.Kasday, J.D.Ullman (1970-1975)
G. Faraci (1974)
A.R.Wilson (1976)
M. Bruno (1977)
等等.除了 Faraci 的实验之外,其余都得出了违反 Bell 不等式, 而与量子力学的预测相符的结果.Faraci 的实验则背离量子的学的预测,而比较接近了 Bell 不等式的极限. 利用单态质子对的实验有一个,是 M.Lamehi-Rachti 及 W.Mittig (1976). 他们的实验也显示出违背 Bell 不等式,而符合量子力学预测的结果. 利用级联光子对的实验比较多,主要有
J.F.Clauser 和 S.J.Freedman (1972)
R.A.Holt 及 F.M.Pipkin (1973)
Clauser (1976)
E.S.Fry 和 R.C.Thompson (1976)
A.Aspect, P.Grangier, G.Roger (1982)
等等.其中 Holt 和 Pipkin 的实验结果违背了量子力学,而符合 Bell 不等式, 其余的皆支持量子力学的预测. 其中较值得注意的是 Aspect 在 1982 年的实验.下图是 Aspect 实验的简图.
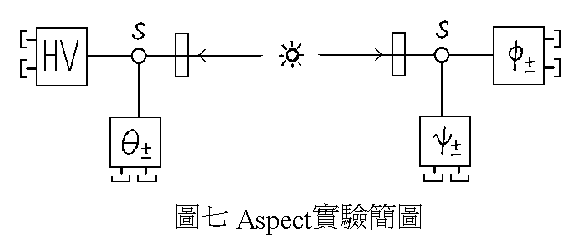
两边各有两个的侦测器可以测量光子的偏极化方向.S 是一超音波开关,以大约 25 MHz 的频率在两个侦测器之间切换著.
在我们前面所谈到的 EPR 实验中,对其中一边粒子的量测会影响到对另一边粒子量测的结果, 换句话说,一边的粒子似乎以某种方式送「讯息」给另一边的粒子.Aspect 的实验装置表明了,如果这样的讯息传递存在的话,其传播的速度将超过光速. Aspect 的实验显示了超距作用(action-at-a-distance)是可能存在的.
至少,到目前为止,实验结果是支持量子力学,而否定 Bell 不等式以及它的前提, Einstein 定域性假设.对此,我们有下面三点评注:
第一,仍有少许实验显示出背离量子力学的结果.然而, 我们以为这是实验系统的误差造成的(例如,注19). 我们这样维护量子力学并不是因为量子力学在原子的领域中是如此的成功, 而是因为,在 Bell 不等式的实验中,量子力学预测了很强的相关性,而 Bell 定理则对此相关性设限.一般的系统误差很容易埋没强烈的相关性而使结果接近 Bell 不等式, 但却不容易加强微弱的相关性.因此,实验技术愈进步,仪器调整愈精确,否定 Bell 不等式的可能就愈大.从最近的实验结果看来正是如此.
第二,所有 Bell 不等式的推导中都或多或少有些辅助性的假设, 这些假设难以直接以实验验证.因此,目前为止还不足以令人完全信服. 然而,即使量子力学将来被证明是错误的,新的理论仍必须面临了违背 Bell 不等式以及解释相隔两地系统相关性的挑战.
第三,虽然 Aspect 等的实验显示了超距作用的可能性, 但这并不表示资讯(information)传递的速度可以超过光速.例如在单态粒子对实验中, 仅有在 A, B 两地的观察者将他们的结果拿来相互比较之后,它们的相关性才会显现出来. 任何一方的观察者无法仅靠他自己侦测器特别的方向而得知对方的安排. 他所看到的结果永远只是一些「正,负,正,负……」交杂出现的乱码.这当中并无任何的资讯可言. |
|
结语 |
|
1985 年,Cornell 大学教授 N.David Mermin 发表了一篇名为「当没有人看月亮时她还在吗?」 (Is the moon there when nobody looks?)的文章,将当代物理学家对 EPR 反论和 Bell 不等式的态度做了一个总结:「在我看来,现在的物理学家可分成两大类, 第一类物理学家饱受 EPR 反论和 Bell 不等式的因扰.而第二类(占大多数)则否. 不过这一类又可分成两小类.2a 类解释他们为什么不受因扰. 然而他们的解释不是完全牛头不对马嘴(如 Born 对 Einstein), 要不然就是包含了一些主张, 稍后可以被证明是错的.2b 类则是不受因扰,也拒绝解释为什么.他们的立场暧昧,无从指责. (2b 类还有一种衍生型,主张 Bohr 已经把一切事情摆平了,但拒绝解释怎么做.)」
物理大师 Richard P. Feynman 在谈到量子力学的基础时也说道:「我找不出真正的问题, 所以我怀疑真正的问题根本不存在.可是我又不能确定没有真正的问题.」
本世纪的两位科学巨人先后去世了.然而这场争论最久,影响层面最广的科学大战并未停止. 相反的,它继续的朝物理学和哲学中更基本,更深远的层面冲击, 向全人类的智慧挑战.这样的冲击和挑战,是否又将会引燃一次更壮烈的革命呢?
且让我们 拭目以待 吧! 全文完....^_^ |
|
注解 |
|
Abraham Pais, Review Modern Physics 51, p863 (1979).
指以互补原理与测不准关系为基础的量子力学非决定论之统计解释.这些观点主要是 Bohr 与 Heisenberg 在 Copenhagen 提出来的,后来逐渐被 Born, Dirac, Pauli 等等许多物理学家所接受. 他们被人们称为 Copenhagen 学派,所以他们对量子力学的解释也就被称为 Copenhagen 解释.
关于 Bohr 对 Einstein 光盒的分析,可见 Stephen Gasiorowicz, Quantum Physics, p37.
A. Einstein, B. Podolsky, N. Rosen, Physical Review 47, p777-780 (15 May 1935).
L. Rosenfeld in Niels Bohr, His Life and Work as Seen by His Friends and Colleagues, S. Rozental, ed., (1967) p114-136.
Niels Bohr, Physical Review 48, p696 (15 Oct 1935).
当然,如果我们坚持只有在两个物理量能够同时被测量时才认为它们同时是实在的,那我们未必会得到 EPR 的结论. 但是,EPR 反驳道,这将使得两个不对易的物理量那一个能被认为是实在的决定于我们将采取何种测量.一个合理的理论不该是如此的.见注 4,p780.
J. Bell: "On the Einstein Podolsky Rosen paradox" Physics I #3, p195 (1964).
后来 Bell 及其后继者都曾改进并推广这个不等式.因此所谓 Bell 不等式并非单一一个不等式,而是此类不等式的通称.
推导这个公式需要量子力学的角动量理论.请参考任何一本量子力学的专书.如 J.J.Sakurai, Modern Quantum Mechanics, p165-168.
Physical Review Letter 23, p880-884 (1969).
吴健雄, L.R.Kasday, J.D.Ullman, Bull. Am. Phys. Soc. 15, p586 (1970); Nuovo Cim. 25, p633-661 (1975).
G.Faraci, S.Gutkowski, S.Notarrigo, A.R.Pennisi, Lett. Nuovo Cim. 9, p607-611 (1974).
A.R.Wilson, J.Lowe, D.K.Butt, J. Phys. G; Nucl. Phys. 2, p613-624 (1976).
M.Bruno, M.d'Agostino, C.Maroni, Nuovo Cim. 40, p142-154 (1977).
M.Lamehi-Rachti, W.Mittig, Phys. Rev. Lett. 14, p2453-2554 (1976).
S.J.Freeclman, J.F.Clauser, Phys. Rev. Lett. 28, p938-941 (1972).
R.A.Holt, F.M.Pipkin, Preprint Harvard University (1973).
J.F.Clauser, Phys. Rev. Lett. 36, p1223-1226 (1976). Clauser 在 1976 年这个实验是重复 1973 年 Holt 和 Pipkin 的方式(见注18),而得到和 Holt 及 Pipkin 相同的结果(违背量子力学).但是 Clauser 发现在实验装置中一个装有电子枪和汞蒸气的 Pyrex 玻璃球(一种耐热玻璃)壁上有不正常的应力.在修正此项错误之后 Clauser 得到了符合量子力学的结果.
E.S.Fry, R.C.Thompson, Phys. Rev. Lett. 37, p465-468 (1976).
A.Aspect, P.Grangier, G.Roger, Phys. Rev. Lett. 49, p91-94 (1982).
A.Aspect, J.Palibard, G.Roger, Phys. Rev. Lett. 49, p1804-1807 (1982).
N.David Mermin, Physics Today April 1985, p41.
Rechard P. Feynman, Simulating Physics with Computers, Int. J. Theo. Phys. 21, p471 (1982). Mermin 将 Feynman 这段评注改写成诗歌的形式,十分有趣:
We have always had a great deal of difficulty
understanding the world view
that quantum mechanics represents.
At least I do,
because I'm an old enough man
that I haven't got to the point
that this stuff is obvious to me
Okay, I still get nervous with it...
You know how it always is,
every new idea,
it takes a generation or two
until it becomes obvious
that there's no real problem
I cannot define the real problem,
therefore I suspect there's no real problem,
but I'm not sure
there's no real problem.
参考资料及推荐读物 要了解 EPR 反论和 Bell 不等式,下面几个是不可不读的好文章: Alastair Rae, Quantum Physics: Illusion or Reality. 1991.
J.J.Sakurai, Modern Quantum Mechanics, p223-241.
David W. Cohen, An Introduction to Hilbert Space and Quantum Logic, Springer-Verlag, 1989, p94-104.
Rae 的那本书非常的浅,几乎不需要任何量子力学的预备知识,所以大一大二学生应也念得懂.Mermin 的文章也不可错过.当然了,别忘了 EPR 的原始论文.
纪念爱因斯坦文集,第一卷,凡异出版社.
探幽入微之路--量子历程,殷正坤著.
柏拉图的天空,邱显正译,天下出版社.
J.F.Clauser, A.Shimony, Bell's theorem: experimental tests and implications, Report Progress in Physics 41, p1881-1927 (1978). Clauser 的这篇文章非常有系统的探讨了到 1978 年为止所进行过检验 Bell 不等式的实验及其结果,非常值得一看. (当然,Aspect 的实验并不包含在内,见注21,22.) | | |
 设为首页
设为首页
 加入收藏
加入收藏