第三节 分组分解法

教学建议

　　1．教材分析：

　　(1)知识结构

　　分组分解法

　　（2）重点、难点分析

　　教学重点和难点

　　重点：分组分解法的分组原则.

　　难点：灵活运用已学过的因式分解的各种方法.

　　（1）分组分解法不是一种独立的分解因式的方法。是为提公因式或运用公式分解因式创造条件，即先把多项式各项适当分组，以达到最后能提公因式或运用公式分解因式的目的，又因为分组无固定的形式，只能教给学生分组的原则，所以分组分解法的原则是本节的重点。

　　（2）分组分解法不是一种独立的分解因式的方法，分组又无固定的形式，要考虑综合运用前面学习的提公因式法或运用公式法两种方法，所以是教学中的难点。

　　1）理解分组分解法在解决因式分解问题中的意义。

　　很多多项式都不能直接运用提公因式法或直接运用公式法分解，但是，进行分组后，就可以先在局部上，进而在整体上运用这两种方法进行分解，使问题迎刃而解。所以，“分组”步骤的作用，在于促进了提公因式法和公式法的应用，使多项式从不能分解的形态向能分解的状态转化．

　　如，多项式 是一个4项式，它的各项没有公因式，而且也没有供4项式作分解的公式可用，所以是用基本方法无法直接分解的多项式．但是，如果运用分组分解法，就可以通过添括号的步骤进行分组，得

原式 ，

　　可以看到，在两个局部上，都是可以用提公因式法分解的．分别分解，得

原式 ，

　　应当注意到，完成了这一步，因式分解并没有完成（想一想，为什么？），但它的意义在于又出现了公因式 ，再从整体上运用提公因式法，可以得

原式 ，

　　从而完成了整体上作分解的目的．

　　所以，在这里，分组分解法的意义在于促进了提公因式法的应用．

　　又如 也是一个不能直接运用基本方法解的多项式，但是，仔细观察式子的特点，作了下面的分组，就打开了分解的大门：

原式 ，

　　这种分组方法使得括号内可以运用公式，得

原式 ，

　　于是，使得整体上形成了再利用公式的态势，从而完成了分解：

　　原式

　　

　　2）能正确分解，要有一定的探索能力．

　　虽然，分组是解决某些多项式分解的钥匙，但并不是每一次分组都能使问题迎刃而解。如前例中，对 如果作下面的分组

原式 ，

　　那么虽然在局部上都可以分别作分解，得

原式 ，

　　但分解在整体上却难以进行下去，因而这种分组实际上没有意义的．

　　所以，在寻求分解的方案时，有可能成功，也可能失败，因而有一定的探索性，试探性，只有具有探索精神的人，肯于多次试验的人，才能筛选出可行的方案．

　　所以只有注意培养自己的探索精神，提高自己的探索能力，才能学好分组分解法．

　　3）要注意正确使用添括号法则．

　　可以看到，分组的过程，就是添括号的过程，所以正确地使用添括号法则，才能正确地选择分组方案，再能正确实现分解．

　　例如，在分解多项式 时，作下面的分组，得

　　原式

　　

　　

　　

　　问题的顺利解决，不仅在于分组的方案正确，而且在于正确地运用了添括号法则：

　　“添加带有正号的括号时，各项都不变号，”如

　　“添加带有负号的括号时，括号内的各项都变号”，如：

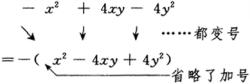
　　应当注意，在处理多项式的过程，有时还要处理去括号的问题，如上例中有

　　

 　　　保留括号

 　　　去括号

　　这也是要十分注意的．

返回页首