第二节 正切和余切

教学建议

　　1.知识结构: 本小节主要学习正切、余切的概念，正切与余切的关系，30°、45°、60°角的正切、余切值，一个锐角的正切（余切）值与它的余角的余切（正切）值之间的关系，以及应用锐角三角函数的知识解决一些简单问题等。

　　2．重点难点分析

　　（1）理解一个锐角的正切、余切值的唯一性，是理解三角函数的核心。

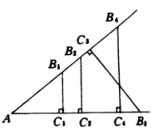
　　锐角的正切、余切与它的正弦和余弦的规定是一样的：当一个锐角确定了，那么这个锐角所在的直角三角形虽然有无穷多个，但它们都是彼此相似的。如上图，当 确定时，包含 的直角三角形有无穷多个，但它们彼此相似：

　　 ∽ ∽ ∽ ……因此，由于相似三角形的对应边成比例，所以这些三角形的对应边的比都是相等的。

　　

　　这就是说，每当一个锐角确定了，包含这个角的直角三角形的上述2种比值也就唯一确定了，它们有确定不变的对应关系。为了简单地表达这些对应关系，我们引入了正（余）切的说法，创造了tan和cot这样的符号。

　　应当注意：单独写出三角函数的符号tan或cot等是没有意义的。因为它们离开了确定的锐角是无法显示出它的含义；另一方面，这些符号和角写在一起时(tan45°)，它表示的就不再是角，而是一个特定的三角形的两条边的比值了（如tan45°=1）。真正理解并掌握这些，才真正掌握了这些符号的含义，才能正确地运用它们。

　　(2) 我们应当学会认识任何位置的直角三角形中的一个锐角的正切、余切的表达式。

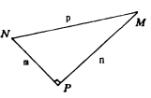
　　我们不仅应当熟练掌握如图那样的标准位置的直角三角形的正切、余切的表达式，而且能熟练地写出无论怎样放置的直角三角形的各三角函数的表达式。如， 如图所示，若 ，则有

，

　　有的直角三角形隐藏在更复杂的图形中，我们也应能正确地写出所需要的三角函数表达式，如图中，ABCD是梯形， ，作 ， 我们应正确地写出如下的三角函数关系式：

　　 ；

　　

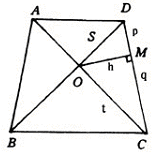
　　很显然，这些表达式提供给我们丰富的边与角间的数量关系。

　　（3）特殊角的正切、余切值既容易导出，也便于记忆，应当熟悉掌握它们。

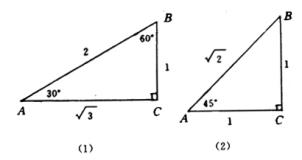
　　利用勾股定理，很容易求出含有 或 角的直角三角形三边的比；如图（1）和图（2）所示。

　　根据定义，有

　　 ,

　　另一方面，可以想像，当 时，边 与AC重合（即 ），所以

　　

　　  由于 无意义而不存在.

　　当 时，边AB与CB重合（即AB=CB），AC的长缩小为0，于是，有

　　

　　 由于 无意义而不存在.

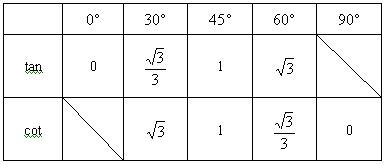
　　把以上结果可以集中列出下面的表：

返回页首