第三节 实数与向量的积

教学建议

知识结构:

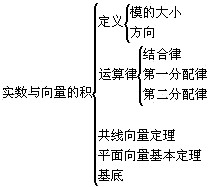
重点难点分析：

　　本节的重点是实数与向量的积的定义、运算律，向量共线的充要条件，平面向量基本定理．向量的加法、减法，实数与向量的积及它们的混合运算称为向量的线性运算，也叫向量的初等运算，是进一步学习向量知识和运用向量知识解决问题的基础．实数与向量的积的结果是向量，要按大小和方向这两个要素去理解．向量共线定理实际上是由实数与向量的积的定义得到的，定理为解决三点共线和两直线平行问题又提供了一种方法．平面向量基本定理体现了数学的化归思想，在几何题目中可以将条件和结论表示为一组向量线形组合的形式，方便问题的解决，另外还为向量的坐标表示提供了理论依据．

　　本节的难点是共线向量充要条件及平面向量基本定理的理解．通过充分性和必要性两个方面的说明，让学生认识定理的本质，向量的共线要与平面中直线的平行区别开．平面向量基本定理通过图形直观得到的，要让学生理解有些困难，另外对于任意一个向量都可用一组基底表示出来，学生刚开始运用可能有难度，要通过练习结合图形逐步理解．

教法建议：

　　1．从实际问题出发引入新课，不但展示了教学的主要内容，而且还激发了学生学习兴趣．如可以通过物理中力与加速度的关系f=ma，位移与速度的关系s=vt等实际问题引入实数与向量的积．

　　2．实数与向量的三个运算律，为了降低难度课本上没有证明，可以结合图形给学生直观解释，程度好的学生可以适当指导给出证明，证明的关键是向量的两要素：方向和大小．

　　3．由于学生已理解共线向量，因此可以让学生观察共线向量间的关系，可以提示从方向和大小两个方面来考虑．然后指出向量共线的充要条件实质上是由实数与向量的积得到的．给学生说明定理的作用，通常用来判断三点在同一条直线上或两直线平行，要指出与平面中直线间的平行的区别．

　　4．平面向量本定理可以从物理上力的分解来引入，学生对于力的分解比较熟悉，使学生首先对定理的应用有所了解．定理是向量坐标表示的基础，因此要学生理解基底的意义．由于不要求证明该定理，只要学生会用即可，所以教学中要侧重于它的应用，培养学生应用所学数学知识的能力．