第四节 双曲线的几何性质

教学建议

教材分析

　　1．知识结构

　　2．重点难点分析

　　重点：双曲线的几何性质，双曲线各元素之间的相互依存关系，特别是双曲线的渐近线性质．难点是有关离心率、渐近线的问题以及双曲线第二定义的应用．关键是要注意数形结合、方程思想及等价转化思想的运用．

　　（1）尽管从双曲线的定义可以分析出双曲线的一些几何性质，但这不是解析几何所要研究的基本问题。我们一定要从双曲线的标准方程出发,仔细研究双曲线的几何性质,如由 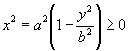，得 ,…；

　　在双曲线方程 中, 以 代换 方程不变,说明双曲线关于 轴对称,…；又由 ，当且仅当 时， 取得最大值 , 所以双曲线的长轴为 , , 为双曲线的两个顶点，等等。

　　我们这样研究双曲线的几何性质，就是想让学生做“用代数的方法研究几何问题”的初步尝试。

　　（2）椭圆与双曲线标准方程和图形、性质对比，如下表

　　（3）对圆锥曲线来说，渐近线是双曲线的特有性质，要重视渐近线的发现和论证过程，明确双曲线渐近线的作用，利用双曲线的渐近线来画双曲线特别方便，而且较为精确，只要作出双曲线的两个顶点和两条渐近线，就能画出它的近似图形．椭圆是封闭曲线，没有渐近线，而双曲线有两条渐线，做出双曲线的渐近线就完全地掌握双曲线的变化趋势．教学双曲线的渐近线时，应注意以下问题：

　　①使学生明确双曲线的渐近线是哪两条直线，过双曲线实轴的两个端点与虚轴的两个端点分别作对称轴的平行线，它们围成一个矩形，其两条对角线所在直线即为双曲线的渐近线，画双曲线时，应先画出它的渐近线．

　　②使学生理解“渐近”两字的含义，当双曲线的各支向外延伸时，与这两条直线逐渐接近，接近的程度是无限的，也可以这样理解：当双曲线上的动点 沿着双曲线无限远离双曲线的中心时，点 到这条直线的距离逐渐变小而无限趋近于0．

　　③使学生掌握根据双曲线的标准方程求出它的渐近线方程的求法．最简单且实用的方法是：把标准方程中“1”用“0”替换得出的两条直线方程，即双曲线 的渐近线方程为 即 ；双曲线 的渐近线方程为 即 ．

　　④使学生掌握根据双曲线的渐近线方程求出双曲线方程的求法．简单且实用的方法是：如果两条渐近线的方程为 ，那么双曲线的方程为 ，这里 是待定系数，其值可由题目中的已知条件确定．

教法建议

　　（1）类比椭圆几何性质的研究方法，引导学生自主探究双曲线的范围、对称性、顶点、离心率等几何性质，要注意椭圆与双曲线性质的区别与联系．

　　（2）对双曲线性质的讨论是我们又一次用曲线方程研究曲线性质的方法的学习，因此，在教学中，应尽力注意让学生对这种方法从思想上有一定的认识，并逐渐形成一种应用意识．

　　（3）教师要引导学生研究双曲线上点的特征，明确双曲线上的点满足双曲线的第一定义，满足双曲线的第二定义，其坐标满足双曲线的标准方程，又满足双曲线的参数方程 .在解决具体问题时, 到底应用哪一条特性, 要因题而议，与两焦点相关问题可考虑第一定义或第二定义；与一个焦点和一条准线相关的问题，可直接利用第二定义，第二定义可以把双曲线上的点与焦点的倾斜距离改为水平距离。

　　（4）教师要带领学生探究直线与双曲线的公共点个数问题，探究的方法是解析法，让学生懂得直线与双曲线的公共点问题，等价于它们对应的二元二次方程组的解的个数问题，又等价于消元后的一元二次方程的根的个数问题，进而，得到处理直线与曲线交点个数的一般方法。基础较好的学生还可以总结直线与曲线相交所得的弦长公式。