第二节 功率

（一）引入课题
　　首先以提问方式复习上一节所学习的主要内容，重点是功的概念和功的物理意义．
　　然后提出力对物体做功的实际问题中，有做功快慢之分，物理学中又是如何来描述的？这节课我们就来研究这个问题．
（二）教学过程
1、功率
　　初中同学们学习过功率的有关知识，都知道功率是用来描述力做功快慢的物理量．我们一起讨论一些问题．
　　力F1对甲物体做功为W1，所用时间为t₁；力F2对乙物体做功为W2，所用时间为t₂，在下列条件下，哪个力做功快？
　　A．W1＝W2，t₁＞t₂；  B．W1＝W2，t₁＜t₂；
　　C．W1＞W2，t₁＝t₂；  D．W1＜W2，t₁＝t₂．
　　上述条件下，哪个力做功快的问题学生都能作出判断，其实都是根据W/t这一比值进行分析判断的．让学生把这个意思说出来，然后总结并板书如下：
功率是描述做功快慢的物理量．
功和完成这些功所用的时间之比，叫做功率．如果用W表示功，t表示完成这些功所用的时间，P表示功率，则：
　　P=W/t
　　明确告诉学生上式即为功率的定义式，然后说明P的单位，W用J、t用s作单位，P的单位为J/s，称为瓦特，符号为W．最后分析并说明功率是标量．
　　接下来着重说明，功率的大小与单位时间内力所做的功为等值．
　　至此，再将功的定义式与速度v的定义式作类比，使学生理解，虽然研究的是不同性质的问题，但是研究方法是相同的(同时也为后面讲瞬时功率做了些准备)．然后提出问题，与学生一起讨论功率的物理意义．
　　上一节我们讲了功的概念、功的公式之后，经过分析和讨论，对功的物理意义已有所了解．谁能复述一下？
　　在学生说出做功过程是能量转化过程之后，立即启发：那么做功快慢恰能表明能量转化的快慢吗？因此，应该将功率理解为是描述做功过程中能量转化快慢的物理量，并将这一认识进行板书．
　　2、平均功率与瞬时功率
　　举例：一个质量是1.0kg的物体，从地面上方20m高处开始做自由落体运动，第1s时间内下落的位移是多少？(与学生一块算出是5m，g取10m/s2)这1s内重力对物体做多少功？(与学生一起算出W1＝50J)第2s时间内物体下落的位移是多少？(15m)这1s内重力对物体做多少功？(W2＝150J)前1s和后1s重力对物体做功的功率各是多大？(P1＝50W，P2＝150W)这2s时间内重力对物体做功的功率是多大？(P＝100W)
　　指出即使是同一个力对物体做功，在不同时间内做功的功率也可能是有变化的．因而，用P＝W/t求得的功率只能反映t时间内做功的快慢，只具有平均的意义．板书如下：
(1)平均功率：
　　P=W/t
(2)瞬时功率
　　为了比较细致地表示出每时每刻的做功快慢，引入了瞬时功率的概念，即瞬时功率是表示某个瞬时做功快慢的物理量．
　　提出瞬时功率如何计算的问题后，作如下推导：
　　一段较短时间内的平均功率可以写成如下公式：
　　P＝W/t=W = F·s/ t， 而s/t=v   
　　所以：P= F·v
　　当t值足够小时，v就表示某一时刻的瞬时速度，所以这时P就表示该时刻的瞬时功率．
　　因此 P＝F·v  就是瞬时功率计算公式
　　讨论：
　　①如果作用于物体上的力F为恒力，且物体以速度v匀速运动，则力对物体做功的功率保持不变．此情况下，任意一段时间内的平均功率与任一瞬时的瞬时功率都是相同的．
　　②很多动力机器通常有一个额定功率，且通常使其在额定功率状态工作(如汽车)，根据P＝Fv可知：
　　当路面阻力较小时，牵引力F也小，v可以大，即汽车可以跑得快些；
　　当路面阻力较大，或爬坡时，需要比较大的牵引力，v必须小．这就是爬坡时汽车换低速挡的道理．
　　③如果动力机器原来在远小于额定功率的条件下工作，例如汽车刚刚起动后的一段时间内，速度逐渐增大过程中，牵引力仍可增大，即F和v可以同时增大，但是这一情况应以二者乘积等于额定功率为限度，即当Fv=P_额．以后，这种情况不可能实现．
　　应用公式P＝Fv计算m＝1kg的物体做自由落体运动中下落1s末和2s末的瞬时功率．
　　由v₁＝10m/s按公式求得P₁＝100J；由v₂＝20m/s按公式求得P₂＝200J．
　　根据上述结果启发学生思考瞬时功率的物理意义．最后指出，此题中是重力对物体做功，使重力势能逐渐向动能转化．随着时间的延续，重力势能向动能转化加快．
　　3、例题讲解
　　例1、如图1所示，位于水平面上的物体A的质量m＝5kg，在F＝10N的水平拉力作用下从静止开始向右运动，位移为s＝36m时撤去拉力F．求：在下述两种条件下，力F对物体做功的平均功率各是多大？(取g＝10m/s2)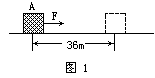

　　(1)设水平面光滑；
　　(2)设物体与水平面间的动摩擦因数μ＝0.15．
　　解答过程可分为三个阶段：
　　①让学生计算力F在36m位移中所做的功，强调功只由F和s这两个要素决定，与其它因素无关，因而两种情况下力F做的功相同，均为W＝360J．
　　②由同学计算这两次做功所用的时间．用牛顿第二定律求出：
　　
　　分别求出t₁＝6s，t₂＝12s．
　　③用功率的定义式即平均功率的计算公式求得P₁＝60W，P₂＝30W．
　　如果有的同学用公式v_t²=2αs分别求出每次的末速度，再用公式：
　　 求出每次的平均速度 和 ，最后用 求得最后结果也可以，并指出这是解决问题的一另一思路。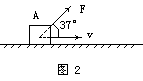
　　例2、如图2所示，位于水平面上的物体A，在斜向上的恒定拉力作用下，正以v＝2m/s的速度向右做匀速直线运动．已知F的大小为100N，方向与速度v的夹角为37°，求：
　　(1)拉力F对物体做功的功率是多大？
　　(2)物体向右运动10s的过程中，拉力F对它做多少功？(sin37°＝0.6，cos37°＝0.8)
　　通过此例题的解答，让学生掌握功率的计算公式P＝Fvcosα，并提醒学生，不要认为F与v总是在同一直线上；并且知道，在功率已知的条件下，可以用W＝P·t计算一段时间内力所做的功．第(1)问的结果为P＝160W；第(2)问的结果为W＝1600J．
　　例3、课本p．139上的例题，注意区分几个概念．
　　 (三)课堂小结
　　1、我们讲了功率概念之后，得到了两个公式，定义式P＝W/t和瞬时功率的公式P＝F·v．
　　2、公式P＝W/t中的t趋近于零时，P即为瞬时功率．不过此公式主要用来计算平均功率．公式P＝Fv中，当v为瞬时速度时，P即为瞬时功率；当v用平均速度 时，也可计算平均功率．当然要注意 所对应的时间段．
　　说明：
　　1、将功率理解为表示能量转化快慢的物理量具有普遍意义．如一台电动机的额定功率是10kW，表明它每秒钟可以将10kJ的电能转化为机械能，不管它是否工作．因而机器的功率实际上可以表示它进行能量转化的能力大小．
　　2、力可以做负功，自然也有负功率．学生不问到时可以不讲．课本上也没讲．重要的不是功率的正负问题，而是要结合实际问题说清楚能量转化的方向和快慢．例如，一物体沿粗糙水平面向前滑动，根据P＝f·v可知其机械能向内能转化，转化的快慢与速度v成正比，这就表达清楚了，没有强调负功率的必要．