第四节 同角三角函数的基本关系式

教学设计方案（一）

同角三角函数的基本关系式

教学目标：

　　1．掌握同角三角函数之间的三组常用关系，平方关系、商数关系、倒数关系．

　　2．会运用同角三角函数之间的关系求三角函数值或化简三角式．

教学重点：

　　理解并掌握同角三角函数关系式．

教学难点：

　　已知某角的一个三角函数值，求它的其余各三角函数值时正负号的选择；

教学用具：

　　直尺、投影仪．

教学步骤：

1．设置情境

　　与初中学习锐角三角函数一样，本节课我们来研究同角三角函数之间关系，弄清同角各不同三角函数之间的联系，实现不同函数值之间的互相转化．

2．探索研究

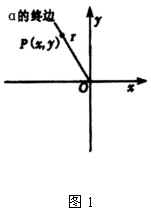（1）复习任意角三角函数定义

　　上节课我们已学习了任意角三角函数定义，如图1所示，任意角 的六个三角函数是如何定义的呢？

　　在 的终边上任取一点 ，它与原点的距离是 ，则角 的六个三角函数的值是：

 ；    ；    

 ；    ；    

（2）推导同角三角函数关系式

　　观察 及 ，当 时，有何关系？

　　当 且 时 、 及 有没有商数关系？

　　通过计算发现 与 互为倒数：∵ ．

　　由于 ，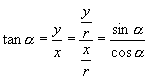

　　这些三角函数中还存在平方关系，请计算 的值．

　　由三角函数定义我们可以看到： ．

　　∴ ，现在我们将同角三角函数的基本关系式总结如下：

　　①平方关系：

　　②商数关系：

　　③倒数关系：

　　即同一个角 的正弦、余弦的平方和等于1，商等于角 的正切，同一个角的正切、余切之积等于1（即同一个角的正切、余切互为倒数）．上面这三个关系式，我们称之为恒等式，即当 取使关系式两边都有意义的任意值时，关系式两边的值相等，在第二个式中， 在第三个式中， 的终边不在坐标轴上，这时式中两边都有意义，以后解题时，如果没有特别说明，一般都把关系式看成是意义的．其次，在利用同角三角函数的基本关系式时，要注意其前提“同角”的条件．

（3）同角三角函数关系式的应用

　　同角三角函数关系式十分重要，应用广泛，其中一个重要应用是根据一个角的某一个三角函数，求出这个角的其他三角函数值．

【例1】已知 ，且 是第二象限角，求 ， ， 的值．

解：∵ ，且 ，∴ 是第二或第三象限角．

　　如果 是第二象限角，那么





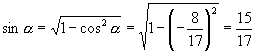
　　如果 是第三象限角，那么 ，

说明：本题没有具体指出 是第几象限的角，则必须由 的函数值决定 可能是哪几象限的角，再分象限加以讨论．

　　【例2】已知 ，求 的值．

　　解： ，且 ， 是第二或第三象限角．

　　如果 是第二象限角，那么

　　

　　

　　如果 是第三象限角，那么 ．

　　说明：本题没有具体指出 是第几象限角，则必须由 的函数值决定 可能是哪几象限的角，再分象限加以讨论．

　　【例3】已知 为非零实数，用 表示 ， ．

　　解：因为 ，所以

　　又因为 ，所以

　　于是     ∴

　　由 为非零实数，可知角 的终边不在坐标轴上，考虑 的符号分第一、第四象限及第二、三象限，从而：





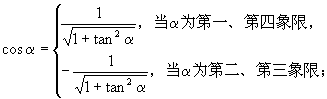
　　在三角求值过程中应尽量避免开方运算，在不可避免时，先计算与已知函数有平方关系的三角函数，这样可只进行一次开方运算，并可只进行一次符号说明．

　　同角三角函数关系式还经常用于化简三角函数式，请看例4

　　【例4】化简下列各式：

　　（1） ；（2） ．

　　解：（1）               （2）

　　　　　　                     

　　　　　　                        

3．演练反馈（投影）

（1）已知： ，求 的其他各三角函数值．

（2）已知 ，求 ， ．

（3）化简：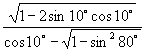

解答：（1）解：∵ ，所以 是第二、第三象限的角．

　　如果 是第二象限的角，则：







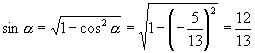
　　又     

　　如果 是第三象限的角，那么

           

      

（2）解：∵    ∴ 是第二或第四象限的角

由【例3】的求法可知当 是第二象限时





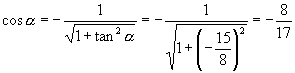
　　当 是第四象限时





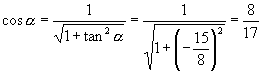
（3）解：原式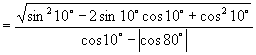

　　　　　　　

　　　　　　　

　　　　　　　

4．本课小结

　　（1）同角三角函数的三组关系式的前提是“同角”，因此 ， ……．

　　（2）诸如 ， ，……它们都是条件等式，即它们成立的前提是表达式有意义．

　　（3）利用平方关系时，往往要开方，因此要先根据角所在象限确定符号，即要就角所在象限进行分类讨论．

课时作业：

1．已知 ， ，则 等于（      ）

　　A．        B．       C．          D．

2．若 ，则 的值是（      ）

　　A．－2        B．2         C．±2            D．

3．化简

4．化简 ，其中 为第二象限角．

5．已知 ，求 的值．

6．已知 是三角形的内角， ，求 值．

参考答案：1．D； 2．B； 3．1； 4． ； 5．3； 6．

注：4．略解：原式

　　　　　　　　　

　　∵ 在第二象限

　　∴

　　∴ ．

6．略解：

　　由 ，平方得， ，

　　∴

　　∵ 是三角形内角

　　∴只有

　　∴ ，

由



　　及 ，联立，得： ， ，

　　∴

教学设计方案（二）

同角三角函数的基本关系式

教学目标：

　　1．应用同角三角函数关系，化简三角式（求值）．

　　2．证明简单的三角恒等式．

教学重点：

　　理解并掌握同角三角函数关系式．

教学难点：

　　（1）三角函数式的化简；（2）证明三角恒等式．

教学用具：

　　投影仪

教学过程：

1．设置情境

　　与代数式的化简求值一样，我们常会遇到大量的结构比较复杂的三角式让你求值，如：“已知 ，求三角式 的值．”就是这样的问题，如果能在求值之前，把三角式进行化简后再求值，那将是非常理想的事．本节课我们就化简、恒等变形等题型与同学们一同展开讨论．

2．探索研究

　　（1）复习同角三角函数关系式

　　上一节课我们已经学习了同角三角函数关系式，请一位同学叙述出同角三角函数的三个关系式．

　　同角三角数关系式有

　　（1）平方关系：

　　（2）商数关系：

　　（3）倒数关系：

下面这组等式也是常用公式，请同学利用定义验证一下．

 ， ，

 ， ， ，

　　化简三角式的基本思路：切、割化弦，和、差化积，“1”去代换等等．证明三角恒等式常用方法：单向证明，双向起动，证等价式等等．

　　代数公式，如 ， ，等也会常用．

（2）例题分析

　　①利用同角三角函数关系式求证三角恒等式及应用

　　【例1】求证

　　证法1：由 知 所以

　　于是   左边 ＝右边

　　∴原式成立

证法2：∵

　　

证法3：∵

　　

　　

　　

      ∴

证法4：设角 终边上任一点 ， ，由定义，

左

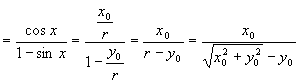
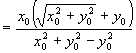
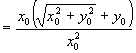
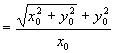
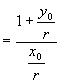
右

　　∴

　　从上例可看出，证明一个等式，可以从它的任何一边开始，证得它等于另一边；还可以先证得另一个等式成立，从而推出需要证明的等式成立．

【例2】求证三角恒等式

证明：左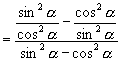边

右边

　　∴等式得证

　　总结，当一个函数式中含有弦、切两类以上的函数，常将“切”函数化为“弦”函数，称为化弦法．

　　【例3】已知 ，求：（1） ；（2） 的值．

　　解：（1）分析1：为了直接利用 ，注意所求值式的分子、分母均为一项齐式（ 、 的次数相同），把分子、分母同除以 （ ），将分子、分母转化为 为元的代数式．

原式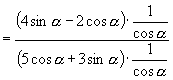

（2）∵

    ∴

    ∴原式

　　　　

　　　　

　　分析2：可利用平方关系 将分子、分母都变为二次齐次式，再利用商数关系式归为关于 的分式求值．

解：原式

　　　　

　　　　

【例4】化简下列各式：

（1） （ 为第三象限角）；

（2）

解：（1）∵ 为第三象限角

∴原式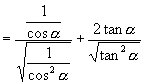

     

注：在运用同角三角函数关系式解题时要特别注意弄清楚角所在象限及其对应的三角函数的符号．

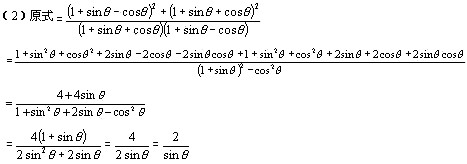
【例5】当 ，求 的值．

分析：本题关键是灵活地多次运用条件等式 从而结合同角三角函数关系式达到降次求解的目标．

解：∵         ∴

　　又∵               ∴

　　∵          ∴

　　∴







3．演练反馈（投影）

1．已知： ，求（1） ．  

（2） 的值．

2．已知： 求 ．

解：1．（1）

　　

　　

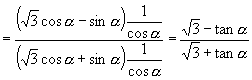
（2）





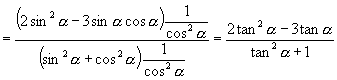
2．解：∵   ①   

　　①两边平方：

　　即       ∴

　　∵     ∴    

　　∴

　　由

　　即

　　

　　∴

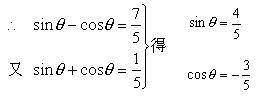
4．本课小结

　　（1）证明同角三角函数恒等式一般有“由繁到简”“中间会师”“变更论证”等方法，具体要求要由等式两端的特征（结构、名称）来选择最佳方法．

　　（2）整体代换、方程思想亦有常用之时．

　　（3）1的代换，往往会给化简、变换化来奇效，有“柳暗花明”之好处．

课时作业：

1．求证：

　　（1）

　　（2）

　　（3）

　　（4）

2．化简

3．设 ，求 ．

4．当 ，（ ）时，化简 的结果是（      ）

　　A． 　　B． 　　C． D．

5．若 ， ，则 的值（      ）

　　A．恒正　　B．恒负　　C．恒为非负　　D．恒为非正

6．已知 ，   求证

参考答案：

1．（1）

　　（2）∵左－右

　　　　　　　　　



  

　　∴左＝右

（3）左 右　∴命题成立

（4）∵

　　∴

2．原式





3．∵



　　∴ ．

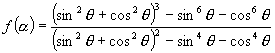
4．由 ， ，

　　得 且

原式



　　∴选C

5．当 ， 时，

　　

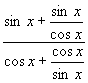
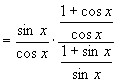
　　∴选A

6．解：消 、 事实上：

　　由

（其中 ， 否则 时或 ， 时，条件均不能同时成立）