第三节 两条直线的位置关系

教学设计方案

课题：点到直线的距离

教学目标：（1）理解点到直线距离公式的推导过程.

　　　　　（2）会求点到直线的距离.

　　　　　（3）在探索点到直线距离公式推导思路的过程中，培养学生发散思维、积极探索的精神.

教学用具：计算机

教学方法：启发引导法，讨论法

教学过程：

一、引入

　　点到直线的距离是指过点 作 的垂线， 与垂足 之间的长度

【问题1】已知点 （-1，2）和直线 ： ，求 点到直线 的距离．

（由学生分析、解答）

　　分析：先求出过 点和 垂直的直线：

 ： ，再求出 和 的交点

　　∴

　　如果把问题1一般化就有如下问题：

【问题2】已知： 和直线 ： （ 不在直线 上，且 ， ），试求 点到直线 的距离．

二、点到直线距离

　　分析1：要求 的长度可以象问题1的解法一样，利用两点的距离公式可以求 的长度．

　　∵ 点坐标已知，∴只要求出 点坐标就可以了．

　　又∵ 点是直线 和直线 的交点

　　又∵直线 的方程已知

　　∴只要求出直线 的方程就可以了.

　　即： ← 点坐标←直线 与直线 的交点←直线 的方程←直线 的斜率←直线 的斜率

　　（这一解法在课前由学生自学完成，课上进行评价总结）

　　问：这种解法好不好，为什么?

　　根据学生讨论，教师适时启发、引导，得出

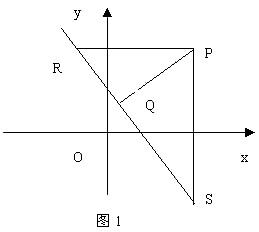　　 分析2：如果 垂直坐标轴，则交点和距离都容易求出，那么不妨做出与坐标轴垂直的线段 和 ，如图1所示，显然相对而言 ，和 好求一些，事实上，设 到直线的距离为 ， 坐标为 ， 坐标为 ，则易求：

，

　　所以： ，

　　所以：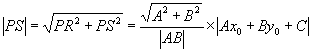

　　根据三角形面积公式：

　　所以： （至此问题2已经解决）

　　公式 的完善.

容易验证（由学生完成）：

　　当 ，即 轴时，公式成立；

　　当 ，即 轴时，公式成立；

　　当 点在 上时，公式成立．

　　公式 结构特点

师生一起总结：

　　（1）分子是 点坐标代入直线方程；

　　（2）分母是直线未知数 、 系数平方和的算术根．

　　类似于勾股定理求斜边的长

三、检测与巩固

　　练习1

　　（1） 到直线 的距离是________．

　　（2） 到直线 的距离是_______．

　　（3）用公式解 到直线 的距离是______．

　　（4） 到直线 的距离是_________．

订正答案：（1）5；（2）0；（3） ；（4） ．

　　练习2

　　1．求平行直线 和 的距离．

　　解：在直线 上任取一点，如 ，则两平行线的距离就是点 到直线 的距离．

　　因此， ＝ ＝

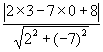【问题3】

　　两条平行直线的距离是否有公式可以推出呢？求两条平行直线 与 0的距离．

　　 解：在直线上 任取一点，如

则两平行线的距离就是点 到直线 的距离，（如图2）．

　　因此， ＝ ＝

　　注意：用公式时，注意一次项系数是否一致．

四、小结作业

　　1、点到直线的距离公式及其推导；

　　师生一起总结点到直线距离公式的推导过程：

　　2、利用公式求点到直线的距离．

　　3、探索两平行直线的距离

　　4、探索“已知点到直线的距离及一条直线求另一条直线距离．

作业：P54  13、14、16思考研究：运用多种方法推导点到直线的距离公式．

五、板书设计

　　略

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　返回页首