 设为首页
设为首页
 加入收藏
加入收藏
教学设计方案(一)
双曲线的几何性质 第一课时
(一)教学目标
1.通过对双曲线标准方程的讨论,掌握椭圆的范围、对称性、顶点、渐近线和离心率等几何性质.
2.了解双曲线中心、实轴、虚轴、渐近线等概念,以及 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的关系及其几何意义.
的关系及其几何意义.
3.通过启发、诱导,让学生明确双曲线性质的研究过程和研究方法,培养学生类比、分析、归纳、猜想、概括、论证等逻辑思维能力.
4.通过类比旧知识,探索新知识,培养学生学习数学的兴趣,探索新知识的能力及勇于创新的精神.
(二)教学过程
【情境设置】
提问(1)前节课根据椭圆的标准方程研究了椭圆的哪几种性质?(如图)
(范围、对称性、顶点、离心率)
(2)请同学说出椭圆 ![]() 的几何性质:
的几何性质:
(学生回答)教师用投影显示下表,并画出焦点在 ![]() 轴上的椭圆
轴上的椭圆
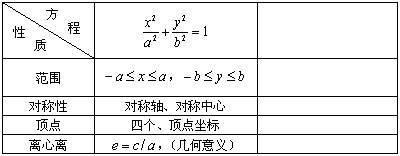
说明:研究双曲线几何性质后,依次在另一纵列填上相应的性质.
上节课已根据双曲线的特征(包括双曲线的坐标系内的位置)导出了双曲线的标准方程,现在我们能根据双曲线的标准方程研究双曲线的几何性质吗?(板书课题)
【探索研究】
1.类比椭圆 ![]() 的几何性质,探讨双曲线
的几何性质,探讨双曲线 ![]() 的几何性质:范围、对称性、顶点、离心率.
的几何性质:范围、对称性、顶点、离心率.
程序是:
学生:自我思考→得出初步结论→小组讨论→得出满意结论→回答所得结论(与大家交流)
教师:启发诱导→点拨释疑→补充完善
列表:

 (教师说明实轴、虚轴、实半轴长、虚半轴长).
(教师说明实轴、虚轴、实半轴长、虚半轴长).
离心率的几何意义下面继续研究图演示
( ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 关系:
关系: ![]() ,
, ![]() )
)
2.渐近线的发现与论证
根据椭圆的上述四个性质,能较为准确地把 ![]() 画出来吗?(能)
画出来吗?(能)
根据上述双曲线的四个性质,能较为准确地把 ![]() 画出来吗?(能)
画出来吗?(能)
通过列表描点,能把双曲线的顶点及附近的点,比较精确地画出来,但双曲线向何处伸展就不很清楚.
我们能较为准确地画出曲线 ![]() ,这是为什么?(因为当双曲线伸向远处时,它与
,这是为什么?(因为当双曲线伸向远处时,它与 ![]() 轴、
轴、 ![]() 轴无限接近)此时,
轴无限接近)此时, ![]() 轴、
轴、 ![]() 轴叫做曲线
轴叫做曲线 ![]() 的渐近线.
的渐近线.
对渐近线并不陌生,例如:
直线 ![]() 是正切函数
是正切函数 ![]() 图像的渐近线.
图像的渐近线.
问:双曲线 ![]() 有没有渐近线呢?如果有,又该是怎样的直线呢?
有没有渐近线呢?如果有,又该是怎样的直线呢?
引导猜想:在研究双曲线范围时,由双曲线标准方程可解出:
![]()
当 ![]() 无限增大时,
无限增大时, ![]() 就无限趋近于零,也就是说,这时双曲线
就无限趋近于零,也就是说,这时双曲线 ![]() 与直线
与直线 ![]() 无限接近.(引导学生分析、猜想)
无限接近.(引导学生分析、猜想)
这使我们有理由猜想直线 ![]() 为双曲线的渐近线.
为双曲线的渐近线.
直线 ![]() 恰好是过实轴端点
恰好是过实轴端点 ![]() 、
、 ![]() ,虚轴端点
,虚轴端点 ![]() 、
、 ![]() ,作平行于坐标轴的直线
,作平行于坐标轴的直线 ![]() ,
, ![]() 所成的矩形的两条对角线,那么,如何证明双曲线上的点的沿曲线向远处运动时,与渐近线越来越接近呢?
所成的矩形的两条对角线,那么,如何证明双曲线上的点的沿曲线向远处运动时,与渐近线越来越接近呢?
显然,只要考虑双曲线在第一象限就可以了.
学生探讨证明方法,教师可给予适当提示,寻找不同证明方法,找学生板演其推理过程,对于基础好一点的学生,可能会得到如下三种证法.(板演其中一种,其他方法用投影给出)
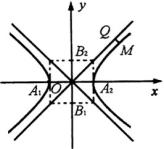 证法一:如图,设
证法一:如图,设
![]() 为第一象限内双曲线
为第一象限内双曲线 ![]() 上的任一点,则
上的任一点,则 ![]() ,
, ![]() 到渐近线
到渐近线 ![]() 的距离为:
的距离为:


点 ![]() 向远处运动,
向远处运动, ![]() 随着增大,
随着增大, ![]() 就逐渐减小,
就逐渐减小, ![]() 点就无限接近于直线
点就无限接近于直线 ![]()
证法二:如图,设 ![]() 为渐近线上与
为渐近线上与 ![]() 有相同横坐标的点,于是
有相同横坐标的点,于是 ![]()

![]()
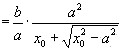
![]()
点 ![]() 沿曲线向远处运动,
沿曲线向远处运动, ![]() 随着增大,
随着增大, ![]() 逐渐减小,于是
逐渐减小,于是 ![]() 也逐渐减小.
也逐渐减小.
证法三:设 ![]() 为渐近线上与
为渐近线上与 ![]() 有相同纵坐标的点,于是
有相同纵坐标的点,于是
![]() ,
, ![]()
∴ ![]()

点 ![]() 沿曲线向远处运动,
沿曲线向远处运动, ![]() 随着增大,
随着增大, ![]() 逐渐减小,于是
逐渐减小,于是 ![]() 也逐渐减小,故把
也逐渐减小,故把 ![]() 叫做双曲线
叫做双曲线 ![]() 的渐近线.
的渐近线.
解决了双曲线向远处伸展时的趋向问题,从而可较准确地画出双曲线,比如画 ![]() ,先作双曲线矩形,画出其渐近线,就可随手画出比较精确的双曲线.
,先作双曲线矩形,画出其渐近线,就可随手画出比较精确的双曲线.
(演示)
3.离心率的几何意义
问:椭圆的离心率反映椭圆的圆扁程度,那么双曲线的离心率有何几何意义呢?
∵ ![]() ,
, ![]() ,∴
,∴ ![]() ,由等式
,由等式 ![]()
可得 ![]()
![]() 越大(接近于1)
越大(接近于1) ![]() 越接近于
越接近于 ![]() 双曲线开口越小(扁狭)
双曲线开口越小(扁狭)
![]() 越大
越大 ![]() 越大
越大 ![]() 双曲线开口越大(开阔)
双曲线开口越大(开阔)
(完善表格)
4.说出双曲线 ![]() 的几何性质.(图形演示)
的几何性质.(图形演示)
5.巩固练习
题1.求下列双曲线的渐近线方程,并画出双曲线.
① ![]() ②
② ![]()
题2.已知双曲线的渐近线方程为 ![]() 且双曲线过点
且双曲线过点
① ![]() ②
② ![]() 分别求出两双曲线方程
分别求出两双曲线方程
然后分别总结两题的解题步骤,最后通过仔细分析,揭示出双曲曲线与其渐近线的方程间的内在变化规律.
双曲线方程: ![]() ,
, ![]()
渐近线方程: ![]()
![]()
一般地,双曲线方程为 ![]() ,它渐近线方程为
,它渐近线方程为 ![]() ,即
,即 ![]() ,反之当渐近线方程为
,反之当渐近线方程为 ![]() 时,它的双曲线方程为:
时,它的双曲线方程为: ![]() .
.
(三)随堂练习
求下列双曲线的实轴和虚轴的长、顶点和焦点坐标、离心率、渐近线方程.
(1) ![]() (2)
(2) ![]()
答案:(1) ![]() ,4,
,4, ![]()
![]()
![]() ,
, ![]()
(2)4,4, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(四)总结提炼
1.双曲线的几何性质及 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的关系,完善上述表格,(投影显示)
的关系,完善上述表格,(投影显示)
2.渐近线是双曲线特有性质,其发现证明蕴含重要的数学思想与数学方法.
3.双曲线的几何性质与椭圆的几何性质有不少相同或类似之处,要注意它们的区别与联系,不能混淆,列表如下:
| 椭圆 |
双曲线 |
|
| 方程 |
|
|
|
|
|
|
| 图形 |
|
|
| 范围 |
|
|
| 对称性 |
对称轴: 对称中心:原点 |
对称轴: 对称中心:原点 |
| 顶点 |
长轴长 |
实轴长 虚轴长 |
| 离心率 |
|
|
| 渐近线 |
无 |
有两条,其方程为
|
(五)布置作业
1.双曲线 ![]() 的( )
的( )
A.顶点坐标是 ![]() ,虚轴端点坐标是
,虚轴端点坐标是 ![]()
B.顶点坐标是 ![]() ,虚轴端点坐标是
,虚轴端点坐标是 ![]()
C.顶点坐标是 ![]() ,渐近线方程是
,渐近线方程是 ![]()
D.虚轴端点坐标是 ![]() ,渐近线方程是
,渐近线方程是 ![]()
2.双曲线的实轴长与虚轴长之和等于其焦距的 ![]() 倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为(
)
倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为(
)
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
3.双曲线中 ![]() ,
, ![]() ,
, ![]() 的长成等差数列,则
的长成等差数列,则 ![]() .
.
4.以椭圆 ![]() 的焦点为顶点,顶点为焦点的双曲线方程是______.
的焦点为顶点,顶点为焦点的双曲线方程是______.
5.已知下列双曲线方程,求它的焦点坐标、离心率、渐近线方程.
(1) ![]() ;(2)
;(2) ![]() .
.
6.求一条渐近线方程是 ![]() ,一个焦点是(4,0)的双曲线标准方程.
,一个焦点是(4,0)的双曲线标准方程.
答案:1.B;2.B;3. ![]() ;4.
;4. ![]() ;
;
5.(1) ![]() ,
, ![]() ,
, ![]()
(2) ![]() ,
, ![]() ,
, ![]() ;
;
6. 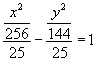 ;
;
(六)板书设计
|
8.4 双曲线的简单几何性质(一) |
||
|
一、复习导入 椭圆的几何性质 二、双曲线的几何性质 1.范围 2.对称性 3.顶点 |
4.渐近线 5.离心率 例题分析 |
渐近的发现与证明 练习小结 |
教学设计示例(二)
双曲线的几何性质 第二课时
(一)教学目标
掌握双曲线的第二定义,双曲线的准线概念.
能利用已知条件熟练地求双曲线的标准方程.
(二)教学过程
【设置情境】
1.提问:双曲线有哪些几何性质?(学生回答、教师板书或投影)
2.说出椭圆的第二定义.(学生回答、教师板书)
平面上点 ![]() 与定点
与定点 ![]() 的距离和它到直线
的距离和它到直线 ![]() 的距离的比是常数
的距离的比是常数 ![]() 的点的轨迹是椭圆.
的点的轨迹是椭圆.
若将上述定义中 ![]() 改为
改为 ![]() 即
即 ![]() 呢?
呢?
【探索研究】
双曲线的第二定义
题目:点 ![]() 与定点
与定点 ![]() 的距离和它到直线
的距离和它到直线 ![]() 的距离的比是常
的距离的比是常 ![]() ,求点
,求点 ![]() 的轨迹.
的轨迹.
解:设 ![]() 是点
是点 ![]() 到直线
到直线 ![]() 的距离,根据题意,所求轨迹就是集合:
的距离,根据题意,所求轨迹就是集合: 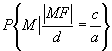
由此得: 
化简得: ![]()
设 ![]() ,就可化为:
,就可化为: ![]() .
.
这是双曲线的标准方程,所以点 ![]() 的轨迹是实轴长、虚轴长分别为
的轨迹是实轴长、虚轴长分别为 ![]() 、
、 ![]() 的双曲线.
的双曲线.
由此可知,当点 ![]() 到一个定点的距离和它到一条定直线的距离的比是常数
到一个定点的距离和它到一条定直线的距离的比是常数 ![]() 时,这个点的轨迹是双曲线.通常称为双曲线的第二定义.定点是双曲线的焦点,定直线叫做双曲线的准线,常数
时,这个点的轨迹是双曲线.通常称为双曲线的第二定义.定点是双曲线的焦点,定直线叫做双曲线的准线,常数 ![]() 是双曲线的离心率.
是双曲线的离心率.
对于双曲线 ![]() ,相应于焦点
,相应于焦点 ![]() 的准线方程是
的准线方程是 ![]() ,根据双曲线的对称性,相应于焦点
,根据双曲线的对称性,相应于焦点 ![]() 的准线方程是
的准线方程是 ![]() ,所以双曲线有两条准线.
,所以双曲线有两条准线.
因此,双曲线离心率的几何意义是双曲线上一点到焦点的距离与到相应准线距离的比.
下面可归纳双曲线的几何性质(教师事先准备一块小黑板,设计如下表格,请两名学生填写,其他学生纠错).
| 标准方程 |
|
|
| 图形 |
|
|
| 范围 |
|
|
| 对称性 |
对称轴: |
|
| 离心离 |
|
|
| 顶点 |
|
|
| 焦点 |
|
|
| 准线 |
|
|
| 渐近线 |
|
|
【例题分析】
例1 已知双曲线方程![]() ,求它的焦点坐标、顶点坐标、离心率、准线方程
和渐近线方程,并画出草图.
,求它的焦点坐标、顶点坐标、离心率、准线方程
和渐近线方程,并画出草图.
可由一位学生演板,其他学生练习,教师巡视.
解:将方程化为标准方程
 可知双曲线的焦点在
可知双曲线的焦点在 ![]() 轴上,且
轴上,且![]() ,
, ![]()
∴ ![]()
∴焦点  ,
,  ,顶点
,顶点 ![]()
![]()
![]() ,准成方程为
,准成方程为 ![]() ,渐近线方程为
,渐近线方程为 ![]() ,方程所表示的图形,如图.
,方程所表示的图形,如图.
例2 求中心在原点,坐标轴为对称轴,一条渐近线的倾斜角为
![]() ,一条准线方程为
,一条准线方程为 ![]() 的双曲线的标准方程.
的双曲线的标准方程.
可让学生练习,教师补充.
解:由题设可知双曲线的焦点在 ![]() 轴上,设双曲线的标准方程为
轴上,设双曲线的标准方程为
![]()
依题设可得
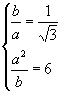 又
又 ![]() 解得
解得 
故所求双曲线的标准方程为
![]()
总评:根据双曲线的准线方程就可确定双曲线的焦点位置,设出方程用待定系数法求 ![]() 、
、 ![]() ,是求双曲线的标准方程的一般思想方法.
,是求双曲线的标准方程的一般思想方法.
例3 已知双曲线与椭圆
![]() 共焦点,它的一条渐近线方程为
共焦点,它的一条渐近线方程为 ![]() ,求双曲线的方程.
,求双曲线的方程.
由一位学生演板,教师归纳以下两种解法:
解法一:由于双曲线的一条渐近线方程为 ![]() ,则另一条为
,则另一条为 ![]() .可设双曲线方程为
.可设双曲线方程为
![]() 即
即 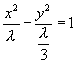
由椭圆方程 ![]() 可知
可知
![]()
双曲线与椭圆共焦点,则 ![]() ∴
∴ ![]() .
.
故所求双曲线方程为 ![]() .
.
解法二:双曲线与椭圆共焦点,可设双曲线方程为
![]()
由渐近线方程 ![]() 可得
可得
![]() ∴
∴ ![]()
故所求双曲线方程为
![]()
点评:1.渐近线为 ![]() 的双曲线方程可表示为
的双曲线方程可表示为 ![]()
2.椭圆 ![]() 与双曲线
与双曲线 ![]()
![]() 有相同的焦点坐标.
有相同的焦点坐标.
例4 双曲线的虚轴长、实轴长、焦距成等差数列,右准线方程是
![]() .且经过点
.且经过点 ![]() .(1)双曲线的离心率
.(1)双曲线的离心率 ![]() ;(2)双曲线的右焦点的轨迹方程.
;(2)双曲线的右焦点的轨迹方程.
分析:这是一道综合题,要灵活运用定义,可教师讲解.
解:(1)依题意,有: ![]() 即
即 ![]()
∴ ![]()
即 ![]() 解得
解得 ![]() .
.
(2)设右焦点为 ![]() ,且点
,且点 ![]() 在双曲线上,由双曲线的第二定义得:
在双曲线上,由双曲线的第二定义得:

即 ![]() 为所求的轨迹方程.
为所求的轨迹方程.
点评:1.要求离心率就要建立关于 ![]() 、
、 ![]() 、
、 ![]() 的方程,若要求离心率的范围,一般要建立关于
的方程,若要求离心率的范围,一般要建立关于 ![]() 、
、 ![]() 、
、 ![]() 的不等式.
的不等式.
2.若题设条件与焦点,准线有关时,一般利用第二定义来解题要方便很多.
(三)随堂练习
1.双曲线 ![]() 的两条准线的距离等于( )
的两条准线的距离等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.如果双曲线 ![]() 上一点
上一点 ![]() 到双曲线右焦点的距离是8,那么
到双曲线右焦点的距离是8,那么 ![]() 到右准线的距离是( )
到右准线的距离是( )
A.10 B. ![]() C.
C. ![]() D.
D. ![]()
3.以曲线的两条准线把两焦点所连线段三等分,则它的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
答案:1.A 2.D 3.B
(四)总结提炼
1.双曲线的第一定义与第二定义是等价的,可以互相推出,双曲线的离心率是焦距与实轴长的比,双曲线上的点到焦点的距离与这点到相应准线的距离的比也是离心率.这也是双曲线的一个几何性质.
2.求双曲线方程要根据具体条件具体对待,确定焦点的位置很重要的.
(五)布置作业
1.准线方程为 ![]() ,离心率为
,离心率为 ![]() 的双曲线的标准方程是( )
的双曲线的标准方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
2.双曲线的两条渐近线的夹角为60°,则双曲线的离心率是( )
A.2或 ![]() B.2 C.
B.2 C. ![]() D.
D. ![]()
3.设双曲线 ![]() 的半焦距为
的半焦距为 ![]() ,直线
,直线 ![]() 过
过 ![]() ,
, ![]() 两点,已知原点到直线
两点,已知原点到直线 ![]() 的距离为
的距离为 ![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.2 B. ![]() C.
C. ![]() D.
D. ![]()
4.与椭圆 ![]() 有公共焦点,且离心离
有公共焦点,且离心离 ![]() 的双曲线方程是________________
的双曲线方程是________________
5.求与定点 ![]() 及定直线
及定直线 ![]() 的距离的比是5:4的点的轨迹方程.
的距离的比是5:4的点的轨迹方程.
6.(1)求渐近线的方程是 ![]() ,经过点
,经过点 ![]() 的双曲线方程.
的双曲线方程.
(2)求渐近线的方程是 ![]() ,实轴长为12的双曲线方程.
,实轴长为12的双曲线方程.
答案:1.C; 2.A; 3.A; 4. ![]() ; 5.
; 5. ![]() ;
;
6.(1) ![]() ,(2)
,(2) ![]() 或
或 ![]()
(六)板书设计
|
8.4 双曲线简单几何性质(二) |
||
|
一、双曲线的第二定义 二、例题分析 例1 例2 |
例3 例4 |
练习 小结 |
教学设计示例(三)
双曲线的几何性质 第三课时
(一)教学目标
1.掌握直线与双曲线位置关系的判定,能处理直线与双曲线截得的弦长,与弦的中点有关的问题.
2.能综合应用所学知识解决较综合的问题,提高分析问题与解决问题的能力.
(二)教学过程
【设置情境】
练习:求下列直线和双曲线的交点坐标(课本P108.5)
① ![]() ,
, ![]()
② ![]() ,
, ![]()
③ ![]() ,
, ![]()
答案:①(6,2),( ![]()
![]() ,)②(
,)②( ![]() ,3)③
,3)③ ![]()
说出上边各例直线与双曲线的位置关系.
不少学生会认为直线 ![]() 与双曲线
与双曲线 ![]() 相切,让学生动手画图,很显然此时直线与双曲线相交,且只有一个交点.
相切,让学生动手画图,很显然此时直线与双曲线相交,且只有一个交点.
为什么会出现这种情况呢?
【探索研究】
直线与双曲线的位置关系
通过对第③小题的研究发现直线 ![]() 与双曲线的渐近线平行,因而此时相交且只有一个公共点.从而得出结论
与双曲线的渐近线平行,因而此时相交且只有一个公共点.从而得出结论
![]()
直线与双曲线相切—只有一个公共点(只有一个公共点是直线与双曲线相切的必要条件,但不是充分条件).
直线与双曲线相离—没有公共点.
【例题分析】
例1 如果直线 ![]() 与双曲线
与双曲线 ![]() 没有公共点,求
没有公共点,求 ![]() 的取值范围.(课本P132第13题)
的取值范围.(课本P132第13题)
解:由 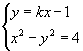 得
得 ![]() 即此方程无解.
即此方程无解.
由  得
得 ![]() 或
或 ![]()
则 ![]() 的取值范围为
的取值范围为 ![]() 或
或 ![]() .
.
引申:(1)如果直线 ![]() 与双曲线
与双曲线 ![]() 有两个公共点,求
有两个公共点,求 ![]() 的取值范围.
的取值范围.
解析:直线与双曲线有两个公共点 ![]() 式方程有两个不等的根
式方程有两个不等的根
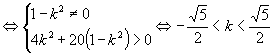 且
且 ![]()
(2)如果直线 ![]() 与双曲线
与双曲线 ![]() 只有一个公共点,求
只有一个公共点,求 ![]() 的取值范围.
的取值范围.
解析:此时等价于(﹡)式方程只有一解
当 ![]() 即
即 ![]() 时,(﹡)式方程只有一解
时,(﹡)式方程只有一解
当 ![]() 时,应满足
时,应满足 ![]()
解得 ![]()
故 ![]() 的值为
的值为 ![]() 或
或 ![]()
(3)如果直线 ![]() 与双曲线
与双曲线 ![]() 的右支有两个公共点,求
的右支有两个公共点,求 ![]() 的取值范围.
的取值范围.
解析:此时等价于(﹡)式方程有两个不等的正根
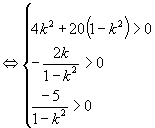 即
即 
(4)如果直线 ![]() 与双曲线
与双曲线 ![]() 的左支有两个公共点,求
的左支有两个公共点,求 ![]() 的取值范围.
的取值范围.
( ![]() )
)
(5)如果直线 ![]() 与双曲线
与双曲线 ![]() 两支各有一个交点,求
两支各有一个交点,求 ![]() 的取值范围.
的取值范围.
解析:此时等价于(﹡)式方程有两个相异实根即 ![]() 即
即 ![]() .
.
例2 直线 ![]() 与双曲线
与双曲线 ![]() 相交于
相交于 ![]() 、
、 ![]() 两点.当
两点.当 ![]() 为何值时,以
为何值时,以 ![]() 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.
可由一位学生演板,教师讲评指出有关二次方程知识的应用.
解:由方程组:  得
得 ![]()
因为直线与双曲线交于 ![]() 、
、 ![]() 两点
∴
两点
∴ ![]()
解得 ![]() .
.
设 ![]() ,
, ![]() ,则:
,则: ![]() ,
, ![]() ,
,
而以 ![]() 为直径的圆过原点,则
为直径的圆过原点,则 ![]() ,
,
∴ ![]() .
.
![]() .
.
于是 ![]() ,
,
即 ![]() .
.
解得 ![]() 满足条件.
满足条件.
故当 ![]() 时,以
时,以 ![]() 为直径的圆过原点.
为直径的圆过原点.
例3 已知双曲线方程
![]() ,试问过点
,试问过点 ![]() 能否作直线
能否作直线 ![]() ,使与双曲线交于
,使与双曲线交于 ![]() 、
、 ![]() 两点,且点
两点,且点 ![]() 是线段
是线段 ![]() 、
、 ![]() 的中点?这样的直线
的中点?这样的直线 ![]() 如果存在,求出它的方程;如果不存在,说明理由.
如果存在,求出它的方程;如果不存在,说明理由.
由学生讨论完成,教师给予提示.
解:假设存在直线 ![]() 满足条件.
满足条件.
显然斜率不存在时,直线 ![]() 不满足条件.
不满足条件.
设 ![]() ,代入双曲线方程整理得:
,代入双曲线方程整理得:
![]()
若 ![]() 即
即 ![]() ,则
,则 ![]() 与渐近线平行,没有交点.
与渐近线平行,没有交点.
∴ ![]() 设
设 ![]() 、
、 ![]() 则:
则: ![]()
由于 ![]() 是
是 ![]()
![]() 的中点.
的中点.
∴ ![]() 解得
解得 ![]() .
.
这时方程为 ![]() ,
, ![]() ,即直线
,即直线 ![]() 与双曲线无交点.
与双曲线无交点.
故这样的直线 ![]() 不存在.
不存在.
例4 已知 ![]() 、
、 ![]() 是过点
是过点 ![]() 的两条互相垂直的直线,且
的两条互相垂直的直线,且 ![]() 、
、 ![]() 与双曲线
与双曲线 ![]() 各有两个交点,分别为
各有两个交点,分别为 ![]() 、
、 ![]() 和
和 ![]() 、
、 ![]() .
.
(1)求 ![]() 的斜率
的斜率 ![]() 的取值范围;
的取值范围;
(2)若 ![]() ,求
,求 ![]() 、
、 ![]() 的方程.
的方程.
由教师讲解,弦长的求法要分步演算.
解:(1)依题意,两直线的斜率都存在,由于 ![]() 与双曲线有两个交点,则下述方程组有两组不同解:
与双曲线有两个交点,则下述方程组有两组不同解:
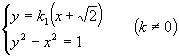 消去
消去 ![]() 得
得 ![]()
于是 ①同理由
①同理由 
得 ![]()
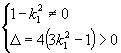
解①②得 ![]() 的取值范围是
的取值范围是 
(2)设 ![]() ,
, ![]() ,则
,则
![]()
![]()
∴ ![]()
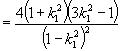
同理 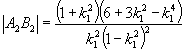
由 ![]() 得
得
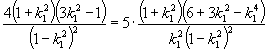
解得 ![]()
当
![]() 时,
时,![]() ,
,![]() ,
,
当 ![]() 时,
时,![]() ,
,![]() .
.
(三)随堂练习
1.设双曲线 ![]() 的左准线与
的左准线与 ![]() 轴的交点是
轴的交点是 ![]() ,则过点
,则过点 ![]() 与双曲线
与双曲线 ![]() 有且只有一个交点的直线共有( )
有且只有一个交点的直线共有( )
A.2条 B.3条 C.4条 D.无数条
2.过双曲线 ![]() 的右焦点
的右焦点 ![]() 作直线
作直线 ![]() 交双曲线于
交双曲线于 ![]() 、
、 ![]() 两点,
两点, ![]() ,则这样的直线
,则这样的直线 ![]() 有( )
有( )
A.1条 B.2条 C.3条 D.4条
3.若过双曲线 ![]() 的右焦点
的右焦点 ![]() ,作直线
,作直线 ![]() 与双曲线的两支都相交,则直线
与双曲线的两支都相交,则直线 ![]() 的倾斜角
的倾斜角 ![]() 的取值范围是__________.
的取值范围是__________.
答案:1.C 2.C 3. ![]()
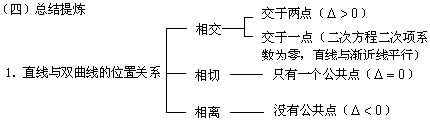
2.注意二次曲线、二次方程、二次函数三者之间的内在联系,直线与双曲线的位置关系通常是转化为二次方程,运用判别式、根与系数关系以及两次方程实根分布原理来解决.
(五)布置作业
1.设双曲线 ![]() 的一条准线与两条渐近线交于
的一条准线与两条渐近线交于 ![]() 、
、 ![]() 两点,相应焦点为
两点,相应焦点为 ![]() ,若
,若 ![]() 为正三角形,则双曲线的离心率为( )
为正三角形,则双曲线的离心率为( )
A. ![]() B.3 C.
B.3 C. ![]() D.2
D.2
2.直线 ![]() 过双曲线
过双曲线 ![]() 的右焦点,斜率
的右焦点,斜率 ![]() ,若
,若 ![]() 与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率
与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率 ![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
3.若过点 ![]() 的直线与双曲线
的直线与双曲线 ![]() 相交于
相交于 ![]() 、
、 ![]() 两点,且
两点,且 ![]() 是线段
是线段 ![]() 的中点,则直线
的中点,则直线 ![]() 、
、 ![]() 的方程是________________.
的方程是________________.
4.直线 ![]() 与双曲线
与双曲线 ![]() 相交于
相交于 ![]() 、
、 ![]() 两点,当
两点,当 ![]() 为何值时,
为何值时, ![]() 、
、 ![]() 两点在双曲线的同一支上?
两点在双曲线的同一支上?
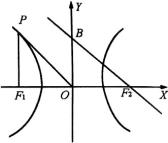 5.过双曲线
5.过双曲线 ![]() 上的点
上的点 ![]() 向
向 ![]() 轴作垂线恰好通过双曲线的左焦点
轴作垂线恰好通过双曲线的左焦点 ![]() ,双曲线的虚轴端点
,双曲线的虚轴端点 ![]() 与右焦点
与右焦点 ![]() 的连线平行于
的连线平行于 ![]() ,如图.
,如图.
(1)求双曲线的离心离;
(2)若直线 ![]() 与双曲线交于
与双曲线交于 ![]() 、
、 ![]() 两点,且
两点,且 ![]() ,求双曲线方程.
,求双曲线方程.
参考答案:
1.D; 2.D; 3. ![]() ;
;
4. ![]() 或
或 ![]() ;
;
5.(1) ![]() (2)
(2) ![]()
(六)板书设计
|
8.2 双曲线的简单几何性质(三) |
||
|
一、引例 二、直线与双曲线的 位置关系 相交 相切 相离 |
例1 引申 例2 |
例3 例4 小结 |