第十节 球

教学设计方案一

9.10 球  第一课时

教学目标：

　　1．理解球的概念，掌握球的性质．

　　2．理解地球经度、纬度、经线、纬线等概念．

　　3．理解球的大圆、两点间的球面距离的定义．

教具准备：     圆规、三角板

教学过程：

[设置情境]

　　1．列举一些球形物体，如足球、篮球、乒乓球、地球仪等，老师强调它是一个面，即整个球面．

　　2．回忆圆的定义：在一个平面内到一个定点的距离为定长的点的集会是一个圆．引导学生结合三维空间的情况对上述结论加以推广，自然得出：在空间内到一个定点的距离为定长的点的集合是一个球面．

　　3．设问：球面还有其他定义吗？什么叫球体呢？球体又会有哪些性质呢？

[探索研究]

　　1．球的概念

　　（教师展示教具，得出球面的旋转定义）

　　半圆以它的直径所在的直线为轴旋转所成的曲面叫做球面，球面所围成的几何体叫做球体．（简称球）

　　（接着教师画出上图，并介绍球的有关概念：球心、球半径、直径、球的表示，特别要强调球面与球二者的区别．）

2．球的性质

　　通过上面的讨论不难看出：球面的两种定义和圆有联系．比如说：从点的集合的观点看圆与球的定义，这个定义就其内容来说，都是指到定点的距离等于定长的点的集合，它们的不同之处只在于定义适用的范围，圆的定义是对平面而言，而球的定义则是对空间而言的，因此可以说，球面的概念是圆的概念在空间的推广，既然如此我们不禁要问，它们之间会不会有某些相似的性质？我们能否从圆的性质去推测并证明球的某些性质呢？

　　（上面的引入和启发为学生对球的性质的进一步探讨在思维方法上做好了必要的准备，学生已形成了一定的“定势”思维．）

　　我们知道圆的割线在圆内的部分为线段，球被平面所截其截面是什么呢？圆面．

　　（教具演示）

　　在圆中，圆心与弦的中点的连线与弦的位置关系是垂直．那么在球中，球心与截面圆心的连线与截面的位置关系是什么呢？

　　（教师画示意图）

　　性质1  球心和截面圆心的连线垂直于截面．

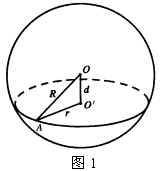
　　性质2  球心到截面的距离 与球的半径 及截面的半径 有下面关系：

　　（演示模型给学生看，不作证明）

　　在圆中，弦心距的变化与弦长有什么关系？

　　当 时弦最长，随着弦心距的增大，弦在减小，当 时弦长为0，这时直线与圆相切．

　　在球中，球心到截面的距离 与截面圆的大小有什么关系？

　　当 时，截面过球心，这时 ，截面圆最大，这个圆叫大圆；当 增大时截面圆越来越小，当 时，截面是小圆，当 时，截面圆缩为一个点，这时截面与球相切．

　　3．地球仪中的经纬度（边演示模型，边讲解）

　　如图2，纬度—— 点的纬度，也是 或 的度数，即：某地的纬度就是经过这点的球半径和赤道平面所成的角度．

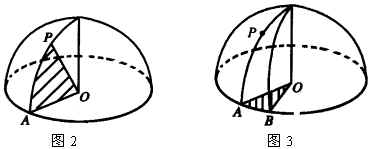
　　如图3，经度—— 点的经度，也是 或 的度数，即：某地点的经度就是经过这点的经线和地轴确定的半平面与本初子午线与地轴确定的半平面所成二面角的平面角的度数．

　　4．球面上两点间的距离

　　平面上两点间的最短距离是连结这两点的线段的长度，而球的表面是曲面，球面上 、 两点间的最短距离显然不是线段 的长度，那是什么呢？

　　（用细线在地球仪上演示）

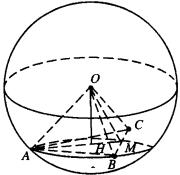
　　如图4， 、 是过 、 的两段劣弧，显然 ，那么这两段弧在本质上有什么区别呢？可以看出，半径不同， 的半径较大，所对劣弧较短，这就启发我们，要找到最短的劣弧，就要找到最大的半径，当然是经过 、 两点的大圆半径 ．在球面上，两点之间的最短连线的长度，就是经过这两点的大圆在这两点间的一段劣弧的长度，我们把这个弧长叫做两点间的球面距离．

　　5．例题分析

　　例1我国首都北京靠近北纬 ，求北纬 纬线的长度．（地球半径约为6370km）

　　（解答见课本第66页）

　　例2  过球半径的中点，作一垂直于这个半径的截面，截面积为 ，求球的半径．

　　解：如图5，为球的轴截面图，设截面半径为 ，球半径为 ，则：   ∴ ， ， ， ，且 ，在 中，由于 ，故由射影定理可知：   即：   解得

　　答：球的半径为 ．

【演练反馈】

　　1． 、 为球面上相异两点，则通过 、 两点可作球的大圆有（   ）

　　A．一个　　B．无穷多个　　C．零个　　D．一个或无穷多个

 　　2．两平行平面截半径为13的球，若截面面积分别为 、 ，则这两个平面间的距离是_______________．

　　3．如图， 、 、 是半径为1的球面上三点， 、 两点间的球面距离为 ，点 与 、 两点间的球面距离均为 ，且球心为 ．

　　求：（l） 、 的大小；

　　　　（2）球心到截面 的距离．

   [参考答案]

1．D　　2.7或 17

3．（1） ， ．

　　（2）取 中点 ，连结 、 ．

　　作 于点 ，证明 ，从而 ，又 ，∴ 面 ，∴ 平面 ∴ 为所求，再证 平面 ， 为正三角形，在 中  ∵ ， ， ，得 .

   [总结锻炼]

　　本节课主要采用类比的思想，由浅入深，循序渐进地启发学生由圆的性质得出球的有关性质，培养学生独立思考、发现问题和解决问题的能力．

 布置作业：课本P71习题9.10   3，4．[参考答案] 3．12cm    4．

板书设计：

9．10 球（一）   1．球的定义        经纬度         3．例题分析   2．球的性质        球面距离       例1 例2 例3

教学设计方案二

9.10 球 第二课时

教学目标：

　　掌握球的体积公式，并能应用公式进行简单计算。

教具准备： 投影胶片

教学过程：

[设置情境]

　　上节课我们学习了球的性质（两条），那么球的体积怎么去求呢？

[探索研究]

　　1．对球的体积公式的推导（图1）

　　（基本思想方法）

　　先用过球心 的平面截球 ，球被截面分成大小相等的两个半球，截面⊙ 叫做所得半球的底面．

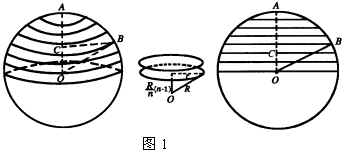
　　（l）分割．

　　用一组平行于底面的平面把半球切割成 层．

　　（2）求近似和．

　　每层都是近似于圆柱形状的“小圆片”，我们用小圆柱形的体积近似代替“小圆片”的体积，它们的和就是半球体积的近似值．

　　（3）由近似和转化为精确和．

　　当 无限增大时，半球的近似体积就趋向于精确体积．

　　（具体过程见课本）

　　2．定理

　　半径是 的球的体积公式为： .

　　3．体积公式的应用

　　求球的体积只需一个条件，那就是球的半径．两个球的半径比的立方等于这两个球的体积比．

　　球内切于正方体，球的直径等于正方体的棱长；正方体内接于球，球的半径等于正方体棱长的 倍（即球体对角钱的一半）；棱长为 的正四面体的内切球的半径为 ，外接球半径为 ．

　　4．例题分析

　　例l  一种空心钢球的质量是142g，外径是5.0cm，求它的内径．（钢的密度是 ）

　　解：设空心钢球的内径为 ，那么钢球质量是：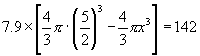

　　解得

　　由计算器算得 　

　　答：空心钢球的内径约为 ．

　　例2  有三个球，一球切于正方体的各面，一球的切于正方体的各棱，一球过正方体的各项点，求这三个球的体积之比．

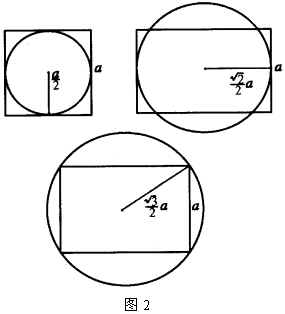
　　分析：本例涉及四个几何体，看似繁杂光绪，但三个球都与正方体有关，故以正方体为主线，分析三个球分别与正方体的关系，得到用正方体棱长表示球半径的关系式．

　　解：设正方体棱长为 ，则由图2可知，与正方体各面相切的球半径 ；与各棱相切的球半径 ；过各项点的球半径为

　　所以，三个球的体积之比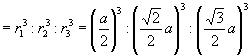

　　例3  求球与它的外切圆柱、外切等边圆锥的体积之比．（提示： ， ）

　　分析：画出它们公共的轴截面，然后寻找几何体与几何体之间元素的关系．

　　解：如图3，等边 为圆锥的轴截面，此截面截圆柱得正方形 ，截球面得球的大圆 ．

　　设球的半径 ，则它的外切圆柱的高为 ，底面半径为 ；

　　 ，

　　

　　∴ ，

　　

　　∴

　　点评：球与旋转体切接时，一般只看它们的轴截面即可解决问题．

[演练反馈]

　　1．课本P69练习1，2．

　　2．如图，半球内有一内接正方体，则这个半球体积与正方体的体积之比为（   ）

　　A．   B．   C．    D．

　　 3．两个半球为1的铁球，熔化后铸成一个球，这个大球的半径为（   ）

　　A．2    B．   C．   D．

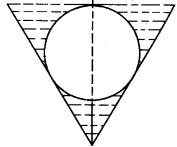
　　4．如图，一个倒圆锥形容器，它的轴截面是正三角形，在容器内放一个半径为 的铁球，并向容器内注水，使水面恰与铁球相切，将球取出后，容器内的水深为多少？

[参考答案]

　　1．略  2．B   3．B  4．

[总结提炼]

　　通常用轴截面图来把立体问题转化为平面问题，所以准确找到符合条件的轴截面图是解题的关键．

布置作业：课本 P 71习题 9.10    5，7，8．

板书设计：

球的体积
1．推导思路 2．球的体积公式	例1 例2	例3 小结	练习

教学设计方案三

9.10 球 第三课时

教学目标：

　　掌握球的表面积公式，并能运用公式进行简单计算．

教具准备：投影胶片．

教学过程：

[设置情境]

　　我们已经用“分割一求和一取极限”的方法求出了球的体积，那么我们也能用类似的方法求出球的表面积吗？

[探索研究]

　　1．球的表面积

　　设球的半径为 ，表面积为 ，体积为 ．

　　我们再次运用推导球的体积公式的方法推导球的表面积公式．

　　（l）分割．

　　把球的表面分成 个小网格，各表面积分别为 ， ，…， ．显然 ．把球心 和每个小网格的顶点连结起来，整个球体就被分为 个“小锥体”，由于底面很小，可以近似看成是“平”的，这时，每个“小锥体”就近似于棱锥，它们的高近似于球半径 ．

　　（2）求近似和．

　　设 个“小锥体”的体积分别为 ， ，…， ，显然，球的体积 ．

　　设第 块“小锥体”底面为 ，高为 ，则体积 ， ，这样就有

及    ①

　　（3）化为准确和．

　　当分割无限加细时，每个小网格无穷小，高 近于趋近于 ．于是，我们由①式得出 的精确值：

         ②

　　由球的体积公式 ，代入②式得：

　　    ∴

　　定理  球的表面积公式为：

　　2．例题分析

　　例1  见课本第70页图1，圆柱的底面直径与高都等于球的直径，求证：

　　（l）球的表面积等于圆柱的侧面积；

　　（2）球的表面积等于圆柱的全面积的 .

　　（解答见课本P70）

　　例2 回答下面问题，并说明理由：

　　（l）球的半径扩大为原来的 倍，它的面积扩大为原来的多少倍？

　　（2）球的面积扩大为原来的 倍，它的半径扩大为原来的多少倍？

　　（3）球大圆的面积扩大为原来的 倍，球面面积扩大为原来的多少倍？

　　（4）球面面积扩大为原来的 倍，球的大圆面积扩大为原来的多少倍？

　　解：设原球半径为 ，面积为 ，

　　（1） ，球面面积扩大为原来的 倍．

　　（2）   ∴ ，半径扩大为原来跳 倍．

　　（3）球大圆面积扩大为原来的 倍得 ， ，球面面积扩大为原来的 倍．

　　（4）球面面积扩大为原来的 倍，半径扩大为原来的 倍，则球的大圆面积为 ，扩大为原来的 倍．

　　例3 如图，正三棱锥高为1，底面边长为 ，内有一球与四个面都相切．

　　求：（l）求棱锥的全面积；

　　　　（2）求球的半径及表面积．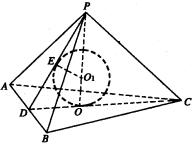

　　解：（l）设过底面中心点 及侧棱 的截面交面 于 ，则 为斜高， 为 中点， ，

　　 中， ，

　　∴

　　（2）设球半径为 ，由 ∽ 得

　　∴

　　答：棱锥全面积为 ，球半径为 ，球表面积为

　　例4  在球内有相距14cm的两个平行截面，它们的面积分别是 和 ，求球的表面积．

　　分析：当截面在球心同侧，截面间距离为球心到截面距离之差；异侧，则为距离之和．

　　解：设球半径为 ．

　　（1）当截面在球心同侧，如图，则有 ，而此方程无解，故截面在球心同侧不可能．

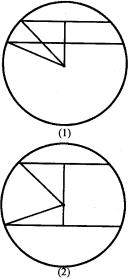
　　（2）当截面在球心异侧，如图，则有 解得 .

　　∴

[演练反馈]

　　1．课本P71练习1，2．

　　2．若球的大圆周长为 ，则这个球的表面积是（   ）

　　A．　　B．　　C．　　D．

　　3．圆锥的底面半径为 ，高为 ，则圆锥外接圆的表面积为___________．

　　4．球面上有四个点 、 、 、 ，如果 、 、 两两互相垂直且 ，求这个球的表面积．

[参考答案]

　　1．略．  2．C   3．    4．

[总结提炼]

　　本节课主要介绍推导球的表面积的方法，并通过例题进一步熟悉球的表面积公式及其应用．

布置作业：

　　1．课本P 72习题 9．10   9，10．

　　2．半径为 的球被两个平行平面所截，截得的两个小圆半径分别是 和 ，求两截面间的距离．

[参考答案]

　　1．略．2． 或 ．（注意分同侧与异侧两种情况．）

板书设计：

教学设计方案四

9.10 球　第四课时

教学目标：

　　1．复习巩固球的有关概念和性质．

　　2．进一步理解经纬度、球面距离等重要概念，并能根据已知条件计算球面上两点间的球面距离．

　　3．巩固掌握球的体积公式与表面积公式．

教学过程：

　　[复习回顾]

　　1．球的性质：

　　2．经纬度

　　3．球面距离

　　4．球的体积公式：

　　5．球的表面积公式：

[探索研究]

　　例1　已知过球面上 、 、 三点的截面和球心的距离等于球半径的一半，且 ，则球面积是（   ）

　　A．    B．   C．    D．

　　解：设球心为 ，⊙ 的圆心为 ，则在三棱锥 中，底面为等边 ，且 。

　　 ，又

　　∴ ，即

　　∴ ，应选D．

　　教师点评：本题最1994年高考题，将已知的各元素集中到正三棱锥中，问题转化为求正棱锥的侧棱长，它就是球的半径．

　　例2  体积相等的正方体、球、等边圆柱的全面积分别为 、 、 ，则它们的大小关系为_______________．

　　解：设正方体边长、球半径、圆柱底面半径分别为 、 、 ，体积为 ，

　　则

　　∴ ， ，

　　∴ ， ，

　　故 ，

    故有 .

　　例3 如图，三棱锥 的两条棱 ，其余各棱长均为5．求三棱锥的内切球的体积．

　　解：取 中点 ，连结 、 ．

　　∵ ，  

　　∴ ， ，

　　∴ 面 .

　　在 中， ， ，

　　∴ ，同理 .

　　∴ ，从而得 .

　　由于各侧面全等，面积均为12，设内切球半径为 ，则

　　∴

　　∴

　　 教师点评：多面体如果有一个内切球，球半径为 ，多面体 个面的面积分别为 ， ， ，…， ，把球心与多面体的顶点连结起来，就把多面体分割成 个以表面为底面， 为高的小棱锥，设多面体体积为 ，则有 ，据此可求球的半径，进而未得球的体积．

　　例4  设地球半径为 ，在北纬 圈上有A、B两地，它们的经度差为 ，求A、B两地的球面距离．

　　解：如图，设球心为 ，北纬 圈的圆心为 ，则 截面 ，

　　∴  ，又 、 两地的经度差为

　　∴ ，在 中，

　　在 中，

　　∴ A、B两地间的球面距离为 .

　　教师点评：求球面上A、B两点间的最短距离（球面距离）的一般步骤是：

　　（l）作出以球心 为顶点的三棱锥

　　（2）计算球心角 的大小（弧度数）．

　　（3）求出大圆上A、B两点间的劣弧的长．

[演练反馈]

　　1．两个球的体积之比是 ，那么这两个球的表面积之比是（  ）

　　A．　　B．　　C．　　D．

　　2．湖面上浮着一个球，湖水结冰后将球取出，冰上留下一个直径为24cm，深为8cm的空穴，则这球的半径为___________．

　　3．已知正三棱往的底面边长为1，侧棱长为2，判断这样的一个三棱柱内能否放进一个体积为的小球．

[参考答案]

　　l．B  2．13   3．不能

布置作业：

1．课本 P 8l  7．　2．课本 P 81  8．

[参考答案]

　　l．如图,取圆柱的轴截面并令 ，则 ， ， ，

　　∴  仅当 时圆柱侧面积最大，最大为

 

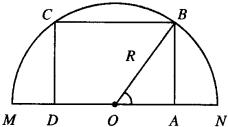
　　2．如图所示取轴截面，设球的半径为 ，则 ，

　　由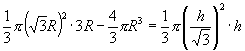

　　解出

板书设计：