第四节 二项式定理

　　掌握二项式定理有其推导方法以及二项展开式的有关特征，并能用它们计算和论证一些简单问题。

教学过程:

【设置情境】

　　问题  某人投资10万元，有两种获利的可能供选择。一种是年利率11％，按单利计算，10年后收回本金和利息。另一种年利率9％，按每年复利一次计算，10年后收回本金和利息。

　　试问，哪一种投资更有利？这种投资比另一种投资5年后可多得利息多少元？

　　分析：本金10万元，年利率11％，按单利计算，10年后的本利和是

10×（1＋11％×10）＝21（万元）

　　本金10万元，年利率9％，按每年复利一次计算，10年后的本利和是

　　那么如何计算 的值呢？能否在不借助计算器的情况下，快速、准确地求出其近似值呢？这就得研究形如 的展开式。

【探索研究】

　　由   

　　

　　那么 

　　展开后，它的各项是什么呢？

　　容易看到，等号右边的积的展开式的每一项，是从每个括号里任取一个字母的乘积，因而各项都是4次式，即展开式应有下面形式的各项：

　　现在来看上面各项在展开式中出现的次数，也就是看展开式中各项的系数是什么？

　　在上面4个括号中：

　　每个都不取b的情况有1种，即 种，所以 的系数是 ；

　　恰有1个取b的情况下有 种，所以 的系数是 ；

　　恰有2个取b的情况下有 种，所以 的系数是 ；

　　恰有3个取b的情况下有 种，所以 的系数是 ；

　　4个都取b的情况下有 种，所以 的系数是 ；

　　因此

。

　　请同学们归纳、猜想

　　一般地，对于任意正整数n，上面的关系式也成立，即有

　　这个公式所表示的定理叫做二项式定理，右边的多项式叫做 的二项展开式。

　　在这里，教师应当指出，上面的定理严格来说是必须证明的，由于知识的局限，以后再证明。

　　二项展开式有以下特征：

　　（1）共有 项。

　　（2）各项里a的指数从n起依次减小1，直到0为止；b的指数从0起依次增加1，直到n为止。每一项里a、b的指数和均为n。

　　利用二项式定理可以求二项展开式。

　　例1  展开 。

　　解： 。

　　例2  展开 。

　　解：先将原式化简，再展开

　　

　　　　　　　

　　　　　　　

　　　　　　　 。

　　例3  用二次式定理证明：

　　（1） 能被100整除；

　　（2） 能被 整除。（ ）

　　证明：（1）∵

　　

　　

　　

　　∴ 能被100整除。

　　（2）可先让学生仿照（1）证明，教师再讲解。

　　∵

　　

　　

　　

　　而   ∴ 是正整数。

　　故 能被 整除。

【演练反馈】

　　1．计算： 。

　　（由一名学生板演后，教师讲解）

　　2．求证： 。

　　（由一名学生板演后，教师讲解）

　　3．求 展开式中含x项的系数。

　　（学生练习后，教师分析讲解）

　　4．解决本节课开始提出的问题。

【参考答案】

1．解：

　　

　　　

　　

　　 。

2．证明：右边

　　

　　 左边

　　故原式得证。

3．解法1：

　　 。

　　显然只有 中含有x项，其系数为

　　 。

　　解法2：由于

　　

　　∴展开式中含x项的系数是

　　 。

　　4．解：

　　

　　

　　由此可见，按年利率9％每年复利一次计算的要比年利率11％单利计算更有利，10年后多得利息1.645万元。

【总结提炼】

　　1．二项式定理是初中学习的多项式乘法的继续，它所研究的是一种特殊的多项式——二项式的乘方的展开式，要理解和掌握展开式的规律。利用它就可以对二项式展开，进行计算或证明。

　　2．对课本第105页这样一段话“容易看到，等号右边的积的展开式的每一项，是从每个括号里任取一个字母的乘积”，要能透彻理解，在解题中适时应用会显得很方便。

板书设计:

教学设计方案二

10．2 二项式定理 第二课时

教学目标：

　　会用二项式的通项公式求展开式中的指定项或指定项系数。

教学过程：

【设置情境】

　　问题  试判断 的展开式中有无常数项？如果有，求出该常数项；如果没有，说明理由。

　　分析：这个问题仅凭观察、想象，无法判断；但展开又嫌太烦且无必要，那么有无良法呢？

【探索研究】

　　1．二项展开式的通项公式

　　二项展开式中的 叫做二项展开式的通项，用 来表示。即通项为展开式的第 项。

　　 。其中 叫做二项式系数。

　　对于 的展开式，其通项公式为

。

　　由于其通项一般记为 ，所以r不是项数， 才是项数；反过来，当已知项数时，将它减去1，才得到r。

　　2．二项展开式的通项公式的作用

　　二项展开式的通项公式，反映出展开式在指数、项数、系数等方面的内在联系，因此能运用二项展开式的通项公式求特定项、特定项系数、常数项、有理项及系数最大、绝对值最大的项。

　　3．例题分析

　　例1  求 的展开式中的倒数第4项。

　　

　　例2  （1）求 的展开式中的第4项的系数；

　　（2）求 的展开式中 的系数。

　　解：（1）展开式的第4项为

　　 　

　　∴第4项的系数是280。

　　（2）设展开式的第 项为含 的项，则

　　

　　∴ 

　　即展开式中的第4项含 ，其系数为

　　 。

【演练反馈】

　　1．求 的展开式中a、b的指数相等的项。

　　（由一名学生板演后，老师指出“某一项”与“某一项系数”的区别）

　　2．解决【设置情境】中的问题。

　　（由一名学生板演后，教师讲评）

　　3．求 的展开式里有多少个有理项？

　　（学生练习后，教师讲解）

　　4．求 的展开式中第3项的二项式系数及第4项的系数。

【参考答案】

　　1．解：设展开式中的第 项a、b的指数相等，则

　　

　　　　

　　依题意得

　　

　　解得 

　　所以a、b指数相等的项是第10项，即

。

　　2．解：假设展开式的第 项为常数项，则

　　

　　依题意

　　

　　故在 的展开式中有常数项，它是第9项，即

　　 。

　　3．解：设展开式的第 项为有理项，则

　　

　　对于一切有理项， 、 必为整数，则r必是6的倍数。

　　又    ，

　　∴

　　     解得 。

　　故 展开式中的有理项有17个。

　　思考：在本题中若问无理项有多少个，如何解决呢？

　　4．解：通项公式为

　　故第3项的二项式系数为

　　第4项的系数为 。

　　注意：二项展开式的二项式系数与该项的（字母）系数是两个不同的概念，前者是指 ，而后者是指除字母外的部分。

【总结提炼】

　　二项展开式的通项公式反映了展开式的一般项，利用它可以求展开式中的任意指定项（如中间项、常数项、整数项、有理项等等）或指定项的系数。

板书设计

教学设计方案三

10．4二项式定理 第3课时

教学目标：

　　掌握二项展开式中的二项式系数的三条性质及有关推导方法，并能简单应用。

教学过程：

【设置情境】

　　在杨辉的《详解九章算术》中载有一个“开方作法本源”图。如图所示，就是“杨辉三角”。那么这个图是如何得来的？它表达的是什么？这节课我们就来共同探讨这个问题！

【探索研究】

　　上节课我们已经知道

　　在二项式定理 中， 叫做二项式系数。

　　它们是一组仅与二项式的次数n有关的 个组合数，而与a、b无关，值得注意的是它们与展开式中的“系数”是有区别的。

　　1．“杨辉三角”的来历及规律

　　 展开式中的二项式系数，当 时，如下表所示：

　　

　　这个表叫做二项式系数表，也称“杨辉三角”。

　　由学生观察这个表的规律，表中每行两端都是1，而且除1以外的每一个数都等于它肩上两个数的和。当n不大时，可以根据这个表来求二项式系数。

　　 展开式的二项式系数依次是

　　从函数角度看， 可看成是以r为自变量的函数 ，其定义域是

　　2．二项式系数的性质

　　1）对称性

　　与首末两端“等距离”的两个二项式系数相等。这一性质可直接由公式 得到。

　　2）增减性与最大值

　　由于

   　

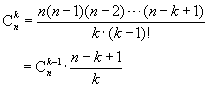
　　所以 相对于 的增减情况由 决定。由

　　 。

　　可知，当 时，二项式系数是逐渐增大的，由对称性可知它的后半部分是逐渐减小的，且中间项取得最大值。

　　因此，当n为偶数时，中间一项的二项式系数 取得最大值；当n为奇数时，中间两项的二项式系数 、 相等，且同时取得最大值。

　　3）各二项式系数的和

　　在二项式定理中，令 ，则

。

　　这就是说， 的展开式的各二项式系数的和等于 。

　　同时由于 ，上式还可以写成

。

　　这是组合总数公式，表示在n个不同元素里，每次取1个、2个、…、n个元素的所有组合数的和。

　　3．例题分析

　　例1  证明在 的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和。

　　证明：在展开式

中，令 ，得

。

　　就是

　　

　　∴ 

　　即在 的展开式中，奇数项的二项式系数和等于偶数项的二项式系数的和。

　　例2    已知 的展开式中，第4项的二项式系数是倒数第2项的二项式系数的7倍，求展开式中x的一次项。

　　解：依题意

　　　　

　　整理得   

　　∴

　　设展开式中含x的项是第 项，则

　　

　　∴   

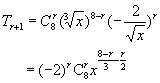
　　解得

　　故展开式中含x的项为第3项，即

　　 。

【演练反馈】

　　1．已知 的展开式中的系数和比 的展开式中的二项式系数和大240，求 的展开式中的第3项。

　　（由一名学生板演后，教师讲评，着重指出“二项式数”与“系数”的区别）

　　2．在二项式 的展开式中，求系数最小的项的系数。

　　3．求 的展开式中系数最大的是第几项？

　　（学生思考后，教师引导分析，展开式中系数最大的项不是中间一项）

　　4．设： 。

　　求： 的值。

　　（学生练习后，教师讲解，指出“取特值”是二项式定理中常用的方法）

【参考答案】

　　1．解：依题意有

　　　　

　　解得

　　于是 的展开式中的第3项是

　　　　

　　　　   

　　2．解：因为在 的展开式中，各项的二项式系数与项的系数相等或互为相反数，又展开式中二项式系数最大的项有两项，分别为第六项 、第七项 ，所以系数最小的项的系数为

　　3．解：设展开式中第 项的系数最大，则

　　

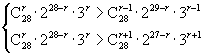
　　即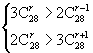     整理得

　　解得   

　　∴

　　故第18项的系数最大。

　　4．解：在

　　令 ，得   

　　令 ，得 

　　两式相乘得

　　　　 。

【总结提炼】

　　二项展开式中的二项式系数都是一些特殊的组合数，它有三条性质，要理解和掌握好，同时要注意“系数”与“二项式系数”的区别，不能混淆，只有二项式系数最大的才是中间项，而系数最大的不一定是中间项，尤其要理解和掌握“取特值”法，它是解决有关二项展开式系数的问题的重要手段。

板书设计

教学设计方案四

10．4 二项式定理 第四课时

教学目标：

　　用二项式定理与二项式系数的性质解答一些简单问题。

教学过程：

【设置情境】

　　 ，是二项式展开式定理，主要研究了以下几个方面的问题：

　　（1）展开式。

　　（2）通项公式。

　　（3）二项式系数及其有关性质。

　　本节课我们就来应用它们解决一些简单的问题。

【探索研究】

　　例1  求 展开式的项数。

　　解：

　　

　　∴ 展开式的项数是

　　

　　例2  已知 的展开式中，第3项的系数与第5项的系数之比是1：4，且第4项等于－1600，求x的值。

　　解：由于

　　

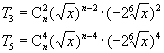
　　依题意有

　　     即

　　∴

　　这时

　　

　　∴

　　解得 。

　　例3  求 的展开式中 项的系数。

　　解：在 中 项的系数为 ，常数项为1

　　在 中 项的系数为 ，常数项为1

　　故在 的展开式中 项的系数为 。

　　（另解）

　　

　　由于积的展开式的每一项，是从每个括号里任取一个字母的积，故展开式中 项的系数为

【演练反馈】

　　1．已知 的展开式中x的系数为19，求：

　　（1）展开式中 系数的最小值；

　　（2）当 的系数最小时，求 的系数。

　　（由一名学生板演后，教师讲评）

　　2．已知二项式 中， 但 。若展开式中的最大系数项是常数项，求 的取值范围。

　　（学生练习后，教师讲解）

　　3．求证： 。

　　（学生思考后，教师讲解）

【参考答案】

　　1．解：（1）由已知得 ，即 ， 。

　　展开式中 的系数是

　　

　　　　　 

　　　　　

　　　　　

　　 且

　　∴当 或 时， 的系数有最小值81。

　　（2）当 的系数有最小值81时， ， 或 ， ，这时 的系数是        。

　　2．解：设展开式中第 项为常数项，由于

　

　　　

　　依题意有

　　　

　　又

　　∴ 代入上式得

　　

　　而

　　∴

　　即展开式中第五项为常数项。

　　由于第五项系数最大，则

　　

　　解得  。

　　3．证明：左边

　　∴ 右边

　　故原式得证。

【总结提炼】

　　二项式定理主要涉及展开式、通项公式、二项式系数或系数，要注意它们的综合运用，对于组合恒等式要分析其特点，正确地选择适当的方法。

（四）布置作业

　　1．已知 的展开式中的前三项系数的和为129，这个展开式中是否含有常数项、一次项？如果没有，说明理由；如果有，求出它们的值。

　　2．设 ，求 的展开式中 的系数。

　　3．已知数列 满足 ，是否存在等差数列 ，使 对一切自然数n均成立？并证明你的结论！

板书设计