第六节 电热的作用

　　[例1]　在电源电压不变时，为了使电炉在相等的时间内发热多些，可采取的措施是 ( )

　　A.增大电热丝的电阻 B.减小电热丝的电阻

　　C.在电热丝上并联电阻 D.在电热丝上串联电阻

　　[分析] 有同学认为应选(A)，根据焦耳定律 Q=I²Rt，导体上放出的热量与电阻成正比，所以要增加热量，可增大电阻.这是由于对焦耳定律理解不全面的缘故.焦耳定律所阐述的导体上放出的热量和某一个量的比例关系是在其他一些量不变的条件下才成立的，如放出的热量和电阻成正比，是指电流强度和通电时间都不变的条件下热量与电阻成正比，按题意，通电时间是相同的，但由于电源电压是不变的，通过电热丝的电流强度将随着电阻的增大而减小，若再根据Q=I²Rt，将不易得出正确的结论.事实上,在电压一定的条件下,根据 可知，减小电热丝的电阻就可增大电功率，即在相同时间内发热多些.

 　　[答]　B.

　　[例2]　有一种双温电炉，其电路图如图2所示，由两段阻值相同的电阻丝组成的发热体，A，B，C为三根引出线，其中A为低温档，B为高温档，且高温档每秒产生的热量是低温档每秒产生热量的2倍，试在方框内画出两段电阻丝的连接图，并说明设计的理由.

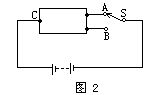
　　[分析]　对纯电阻电路，电流通过导体发热.当电压恒定时，可选用 来考虑.由于t相等,电流的发热Q与电阻R成正比.若高温档的发热是低温档的2倍,则高温档的电阻值是低温档的二分之一.

　　 　

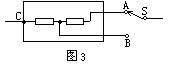
　　[答]　方框内的两段电阻丝应如图3连接.

　　设计合理性证明如下：

　　当S接高温档BC时，

　　

　　当S接低温档AC时，

　　

　　可见设计合理.

　　[例3]　有两根电阻丝，当只给一根通电时，需要t₁分钟才能煮沸一壶水，当只给另一根通电时，需要t₂分钟才能煮沸一壶水，已知t₂﹥ t₁，若将这两根电阻丝串联起来使用，则煮沸一壶水的时间为t， 若将这两根电阻丝并联起来使用，则煮沸一壶水的时间为t’.

　　求t和  t’.

　　[分析]  烧开同一壶水需要吸收热量相同，电源电压相同. 根据Q=(U²/R)t求出每一根电阻丝的电阻，把两根电阻丝串联后的总电阻、并联后的总电阻求出.分别煮沸一壶水的时间就求出来了.

　　解：根据Q=(U²/R)t

   　　　　　　R₁= (U² / Q) t₁

　　　　　　R₂= (U² / Q) t₂

　　串联后的总电阻R= R₁+ R₂= (U² / Q) t₁+ (U² / Q) t₂

　　煮沸一壶水的时间t= Q/(U²/R)= {Q [ (U² / Q) t₁+ (U² / Q) t₂]}/ U²= t₁+ t₂

　　并联后的总电阻R’和t’同理也可求出.