第一节 冲量和动量

典型例题

冲量相等时物体的运动情况

　　例1如果物体在任何相等的时间内受到的冲量都相同，那么这个物体的运动（   ）．

　　A、可能是匀变速运动

　　B、可能是匀速圆周运动

　　C、可能是匀变速曲线运动

　　D、可能是匀变速直线运动

　　分析与解：冲量是力与时间的乘积，在任何相等的时间内冲量都相同，也就是物体受到的力恒定不变，所以物体做匀变速运动，其轨迹可以是直线的也可以是曲线的．答案为A、C、D．

下落物体的重力冲量

　　例2　 一个质量为5kg的物体从离地面80m的高处自由下落，不计空气阻力，在下落这段时间内，物体受到的重力冲量的大小是（    ）．

　　A．200N·s    B．150N·s     C．100N·s    D．250N·s

　　分析与解：根据冲量的定义 在这个过程中重力的大小是一个定值，只需求出这个过程所用的时间即可．



　　答案：C．

冲量公式的简单应用

　　例3 一匹马通过不计质量的绳子拉着货车从甲地到乙地，在这段时间内，下列说法中正确的是：（     ）．

　　A、马拉车的冲量大于车拉马的冲量

　　B、车拉马的冲量大于马拉车的冲量

　　C、两者互施的冲量大小相等

　　D、无法比较冲量大小

　　分析与解：在这个过程中，马对车的拉力，与车对马的拉力是一对作用力与反作用力，大小总是相等的，根据冲量的定义，时间也相同，所以冲量的大小是相等的．

　　答案：C．

关于动量的矢量计算

　　例4 质量为5kg的小球以5m／s的速度竖直落到地板上，随后以3m／s的速度反向弹回，若取竖直向下的方向为正方向，则小球动量的变化为（    ）

　　A．10kg·m／s           B．－10kg·m／s

　　C．40kg·m／s           D．－40kg·m／s

　　分析与解：动量的变化是末动量减去初动量，规定了竖直向下为正．

　　初动量 kg·m/s

　　末动量 kg·m／s

　　动量的变化 kg·m／s

　　答案：D．

关于抛体运动物体的重力冲量

　　例5 质量为5kg的小球，从距地面高为20m处水平抛出，初速度为10m／s，从抛出到落地过程中，重力的冲量是（      ）．

　　A．60N·s    B．80N·s     C．100N·s       D．120N·s

　　分析与解：在这个过程中，小球所受重力恒定不变，只需求出这个过程的时间即可



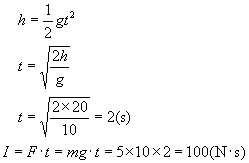
　　答案：C．

动量大小与速度的关系

　　例6 质量为60kg以1m/s速度步行的人和以800m/s速度飞行的质量为0.01kg的子弹，哪个动量大？

　　解：人

　　子弹

　　即：人的动量大．

课本例题分析与设疑

　　例7 一个质量是0.1kg的钢球，以6 m／s的速度水平向右运动，碰到一个坚硬的障碍物后被弹回，沿着同一直线以6m／s的速度水平向左运动（如图）．碰撞前后钢球的动量有没有变化？变化了多少？

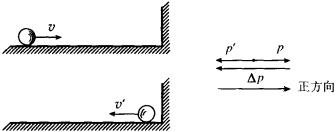
　　分析：动量是矢量，它的大小和（或）方向发生了变化，动量就发生了变化，碰撞前后虽然钢球速度大小没有变化，都是6m／s，但速度的方向发生了变化，动量的方向与速度的方向相同，动量的方向也发生了变化，所以钢球的动量发生了变化．

　　解：取水平向右的方向为正方向，碰撞前钢球的速度 m/s，碰撞前钢球的动量为：

　　碰撞后钢球的速度 m/s，碰撞后钢球的动量为

　　碰撞前后钢球动量的变化为

　　动量的变化 也是矢量，求得的数值为负值，表示 的方向与所取的正方向相反， 的方向水平向左。

结论：碰撞前后物体仍在同一条直线上运动，可先设一个正方向，末动量 和初动量p可据此用正、负值表示，则动量的变化 却可用代数方法求出．

设疑：若碰撞前后物体不在同一条直线上运动，那么动量的变化又如何求呢？

课本思考与讨论的分析

　　例8 思考与讨论：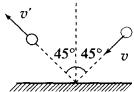

　　如图所示，一个质量是0.2kg的钢球，以2m/s的速度斜射到坚硬的大理石板上，入射的角度是45°，碰撞后被斜着弹出，弹出的角度也是45°，速度仍为2m/s，你能不能用作图法求出钢球动量变化的大小和方向？

　　本书虽然不要求作这种计算，但是思考一下这个问题，会帮助你进一步认识动量的矢量性．

　　分析：（如图）动量是矢量，动量方向与速度方向相同，我们可以用作图法（如图）根据平行四边形定则求动量变化 ．

          

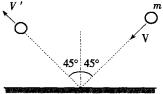
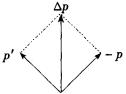
　　根据 可求得 kg·m／s，方向竖直向上．

　　结论：碰撞前后物体不在同一条直线上运动，可用作图法，根据平行四边形定则，以p和－p为邻边，作出平行四边形，其对角线长与 大小成正比，方向就是 的方向．

返回页首