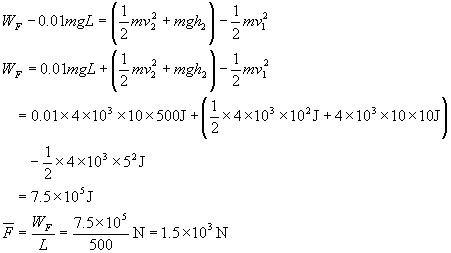设为首页
设为首页
 加入收藏
加入收藏
典型例题 (例1~例4)
例1 气球受到的浮力为其重量的1.5倍,由地面上升到离地40米高处时,由气球上脱离出一个物体,问从物体脱离气球时起,再经过多少时间此物体的动能恰为其势能的两倍?(取g=10米/秒2)
选题目的:本题对于学生掌握整体分析法解题有帮助
揭示思路:首先要把整个体系的运动过程搞清楚,气球从地面上开始作初速为零的匀加速直线运动,在40米高处它获得了速度![]() ,此时物体的脱离出,可看作是一个由脱离点以
,此时物体的脱离出,可看作是一个由脱离点以![]() 速度上抛的物体。
速度上抛的物体。
设物体运动到C点时的动能恰为势能的两倍。这样我们就得先判断C点是在A点的上方还是下方。
物体在A点时的热能![]()
而动能![]()
![]()
![]()
因此EKA<EPA。所以在A点上方,物体越上升EP将越大,EK将越小。所以只有物体再落至A点以下C点时才有可能实现EKA=2EPC(如图)
解法1,可分段运算。
先计算物体由A→B的上升高度和所用时间:物体从A点脱离气球是以![]() 初速做竖直上抛运动,所以要先求
初速做竖直上抛运动,所以要先求![]() 。气球从地面上升,是浮力做正功,重力做负功,那么获得功能:
。气球从地面上升,是浮力做正功,重力做负功,那么获得功能:
![]()
![]() 消去M得
消去M得![]()
所以:![]()
物体上抛至最高点B位移为
![]()
则体从A→B所用时间:
![]()
然后再计算物体从B落至C的情况:
根据题意可知是物体在高度为60米处自由下落,在C处其EKC=2EPC,这样我们就可以利“思维基础7”的例子的解法,求出C点距地面的高度hc。
因为EKC=2EPC
所以C点机械能总量为EC=3EPC
根据机械能守恒定律知:EB=EC
即mghB=3mghc
∴hc=![]() hB=20米
hB=20米
则物体从BC的位移为40米。
因此下落时间为![]()
那么总时间t=t上+t下=4.83秒
解法2:根据EKC=2EPC
可知:![]()
你可以利用运动学的规律求出vc和hc来,代入上式即可求出。你试一试。
你可能还会创造一些解法,这是培养你创造性能力的好方法,你不妨动一动脑子。
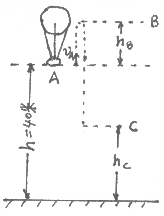
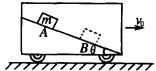
例2 固定在火车车厢内的光滑斜面,倾角为![]() ,车厢以速度
,车厢以速度![]() 前进,斜面上质量为m的滑决从点A自由下滑距离为s,如图所示.试分析:以地面为参照系,质量为m的滑块机械能是否守恒?
前进,斜面上质量为m的滑决从点A自由下滑距离为s,如图所示.试分析:以地面为参照系,质量为m的滑块机械能是否守恒?
选题目的:注意不同参照系中机械能守恒的问题
解析:以地面为参照系,取过A点的水平面为零势能面,则
![]()
![]()
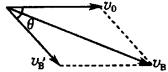
式中![]() 为滑块从点A相对斜面下滑距离s,后到达点B时相对地的速度,其大小为滑块在点B时相对车厢的速度
为滑块从点A相对斜面下滑距离s,后到达点B时相对地的速度,其大小为滑块在点B时相对车厢的速度![]() 和车厢速度
和车厢速度![]() 的矢量和的大小,
的矢量和的大小,![]() 和
和![]() 夹角为
夹角为![]() .
.
如图所示,以车厢为参照物,滑块从点A下滑到点B的过程中,只有重力做功,根据机械能守恒定律,得
![]()
由余弦定理,得
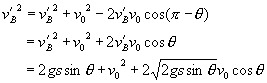
将上述表达式,代入![]() 式中,有
式中,有
![]()
即
![]()
故以地面为参照系,质量为m的滑块机械能不守恒.
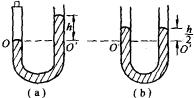
例3 粗细均匀的U形玻璃管,竖直放置,将其左侧开口用软橡皮塞封住,从右侧开口注入适量水银后,经测量,两侧水银面高度差为h,水银柱总长为4h,如图(a)
轻轻地将橡皮塞拔出,试问:两侧水银面平齐时,液面上升(下降)的速度多大(不计水银在管中运动时所受的阻力)?
选题目的:对于学生把握机械能守恒定律在流体及非固联物系统中的应用有一定的帮助。
分析与解 :
由于水银在玻璃管中流动时阻力很小,可以不计,故机械能守恒.
开始时右侧水银面比左侧面高h,取左侧水银面所处水平面![]() 为重力势能参照面(如图(a)),这时右侧管中参照面上方长度为h的水银柱的重力势能为
为重力势能参照面(如图(a)),这时右侧管中参照面上方长度为h的水银柱的重力势能为
![]()
由于参照面下方总有长度为3h的水银柱、它的重力势能不发生变化,可以不予考虑,
拔去橡皮塞,在重力作用下右侧水银面下降,左侧水银面上升,设两侧水银面平齐时,水银柱的速度为v,这时整个水银柱的动能为
![]()
这时,参照面上方两段水银柱的重力势能为
![]()
根据机械能守恒定律,![]() ,即
,即![]() 。将上述
。将上述![]() 及
及![]() 表达式代入,经化简可得两侧水银面平齐时,水银面上升(下降)的速度为
表达式代入,经化简可得两侧水银面平齐时,水银面上升(下降)的速度为
![]()
例4 如图所示,小铁球A、B分别固定在长度均为L的轻线、轻杆的下端,线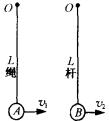 、杆的上端分别固定于O点,且均能绕O点无摩擦地转动.要求小球能绕过最高点,求小球在最低点的最小速度
、杆的上端分别固定于O点,且均能绕O点无摩擦地转动.要求小球能绕过最高点,求小球在最低点的最小速度![]() 、
、![]() 各为多大?
各为多大?
选题目的:对于学生掌握机械能守恒定律在圆周运动的应用有一定的帮助
分析:线或杆对小球的弹力,在小球绕O点做圆周运动的过程中,始终与瞬时速度相垂直,所以弹力不做功.只有重力作功,小球的机械能守恒.要注意到线与杆对球约束的差异,线可受拉力不能受压力.所以A球达最高点线的拉力的最小值为零,线不可能给小球以支持力,球速不能小于![]() ;杆可受拉力也可受压力,所以B球达最高点杆可以给小球以支持力,球速允许等于零.
;杆可受拉力也可受压力,所以B球达最高点杆可以给小球以支持力,球速允许等于零.
解:要求A球作圆周运动达到最高点,并具有最小的速度,则要求线处于要松的临界状态,即拉球的弹力等于零的状态.A球在最高点由所受的重力提供向心力.
由牛顿第二定律得![]()
由机械能守恒定律,设球的最低点重力势能为零,则![]()
![]() 的最小值为
的最小值为![]()
要求B球达到最高点,且具有最小的速度,则由于杆可以给球支持力F,当![]() 时,
时,![]() 。
。
由机械能守恒定律得 ![]()
![]() 的最小值为
的最小值为![]()
点评:在解答有关竖直面内的圆周运动时,一定要注意临界条件的判断,物体能否作完整的圆周运动,关键在于能否通过最高点.绳子约束的物体,通过最高点的临界条件是弹力等于零,而速度不等于零;杆约束的物体,通过最高点的临界条件是速度等于零两弹力不等于零.
典型例题 (例5~例7)
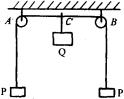
例5 如图所示,质量不计的长绳,沿水平方向跨放在相距2L的两个小滑轮A和B上,绳的两端各挂一个质量均为m的物体P;若将质量为M(![]() )的物体Q,挂在AB的中点C处并由静止释放,求Q沿竖直方向下落的最大距离(不考虑滑轮的质量及摩擦力).
)的物体Q,挂在AB的中点C处并由静止释放,求Q沿竖直方向下落的最大距离(不考虑滑轮的质量及摩擦力).
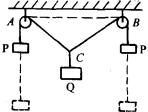
选题目的:对于学生领会机械能守恒定律在滑轮系统的应用有较大的帮助。
分析与解: 把物体P和物体Q以及连接它们的绳子作为一个系统,运动中只有重力做功,故系统机械能守恒.
系统由静止开始,当Q沿竖直方向下降最大距离H时,速度显然为零.这时两个物体P沿竖直方向上升h,它们的速度也为零(如图所示);不难看出
![]()
Q下降,重力势能减少MgH;两个物体P上升,重力势能增加2mgh;根据机械能守恒定律有
![]()
解上式,可得![]()
【综合评述】
①重物Q下降到最低点时,速度为零,但这时它的加速度不为零!Q下降到最低点时,它所受的合外力竖直向上,Q有竖直向上的加速度!同样,旁边两个物体P有竖直向下的加速度.
②为了说明问题,并使读者能获得较为明确、深刻的印象。假定![]() ,在此条件下,
,在此条件下,![]() 。
。
在![]() 的条件下,系统的平衡位置即物体P、Q所受合外力为零位置在什么地方呢?
的条件下,系统的平衡位置即物体P、Q所受合外力为零位置在什么地方呢?
不难判断,P、Q所受合外力为零时,绳中张力![]() ,对Q来讲,它受绳AC、BC的拉力的合力和重力作用:
,对Q来讲,它受绳AC、BC的拉力的合力和重力作用:![]() ,即
,即![]() ,可知这时绳AC、BC与竖直方向的夹角〔
,可知这时绳AC、BC与竖直方向的夹角〔![]() ,即绳AC、BC间的夹角〕为120°;这时物体Q与最高位置之间的距离
,即绳AC、BC间的夹角〕为120°;这时物体Q与最高位置之间的距离
例6 如图所示,已知光滑水平面上的光滑斜面体质量为m,铁球的质量也为m,球心与悬点之间的距离为L,斜面体在水平力作用下,系统恰好处于静止状态,这时悬挂铁球的细绳与竖直方向的夹角等于![]() 。撤去水平力F,斜面体最终将以速度v沿光滑水平面做匀速运动;铁球将来回摆动,摆动时最高位置与最低位置的高度差为h。求解v和h的值:
。撤去水平力F,斜面体最终将以速度v沿光滑水平面做匀速运动;铁球将来回摆动,摆动时最高位置与最低位置的高度差为h。求解v和h的值:
选题目的:学生领会机械能守恒定律的优点和温习运动学知识有较大的帮助。
分析与解:
(1)由于斜面体和水平面都光滑,撤去F后,摆球和斜面体组成的系统,只有摆球所受的重力做功,故系统机械能守恒。
撤去水平力F后,斜面体沿光滑水平面向右运动.摆球沿圆弧运动;当摆线到达竖直位置时,摆球与斜面体的水平速度(设为v)相等,由机械能守恒定律可知
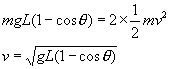
(2)斜面体与摆球分离后,摆球系统的总能量为![]() ,振动中机械能守恒,动能与重力势能相互转化,摆球的最高位置与最低位置的高度差h由机械能守恒定律决定:
,振动中机械能守恒,动能与重力势能相互转化,摆球的最高位置与最低位置的高度差h由机械能守恒定律决定:
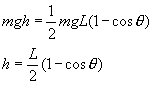
例7 质量![]() kg的汽车开上一山坡。汽车沿山坡每前进100m,其高度升高2m。上坡时汽车速度为5m/s,沿山坡行驶500m后速度变为10m/s。已知车行驶中所受阻力大小是车重的0.01倍,试求:
kg的汽车开上一山坡。汽车沿山坡每前进100m,其高度升高2m。上坡时汽车速度为5m/s,沿山坡行驶500m后速度变为10m/s。已知车行驶中所受阻力大小是车重的0.01倍,试求:
(1)此过程中汽车所受牵引力做功多少?
(2)汽车所受平均牵引力多大?取![]() 。
。
选题目的:对于学生理解功能原理和动能定理的区别有较大的帮助。
引导学生思考与分析:
(1)如何依据![]() 求解本题?应用该规律求解问题时应注意哪些问题?
求解本题?应用该规律求解问题时应注意哪些问题?
(2)用![]() 求解本题,与应用动能定理
求解本题,与应用动能定理![]() 有什么区别?
有什么区别?
归纳学生分析的结果,教师明确给出例题求解的主要过程:
取汽车开始时所在位置为参考平面,应用物体机械能变化规律![]() 解题时,要着重分析清楚重力、弹力以外其它力对物体所做的功,以及此过程中物体机械能的变化。这既是应用此规律解题的基本要求,也是与应用功能定理解题的重要区别。
解题时,要着重分析清楚重力、弹力以外其它力对物体所做的功,以及此过程中物体机械能的变化。这既是应用此规律解题的基本要求,也是与应用功能定理解题的重要区别。