第四节 单摆

典型例题

　　例1：关于单摆的说法，正确的是（  ）

　　A．单摆摆球从平衡位置运动到正的最大位移处时的位移为A（A为振幅），从正的最大位移处运动到平衡位置时的位移为－A．

　　B．单摆摆球的回复力等于摆球所受的合外力

　　C．单摆摆球的回复力是摆球重力沿运动轨迹切线方向的分力

　　D．单摆摆球经过平衡位置时加速度为零

　　出题目的：此题主要考查单摆摆动中的回复力掌握情况.

　　解析：简谐运动中的位移是以平衡位置作为起点，摆球在正向最大位移处时位移为A，在平衡位置时位移应为零，摆球的回复力由合外力沿圆弧切线方向的分力（等于重力沿圆弧切线方向的分力）提供，合外力在摆线方向的分力提供向心力，摆球经最低点（振动的平衡位置）时回复力为零，但向心力不为零，所以合外力不为零，（摆球到最高点时，向心力为零，回复力最大，合外力也不为零）．

　　正确选项为C．

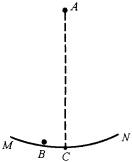　 　　例2：如图所示，MN为半径较大的光滑圆弧轨道的一部分，把小球A放在MN的圆心处，再把另一小球B放在MN上离最低点C很近的B处，今使两球同时自由释放，则在不计空气阻力时有（  ）．

　　A．A球先到达C点　　B．B球先到达C点

　　C．两球同时到达C点　　D．无法确定哪一个球先到达C点

　　出题目的：此题考查单摆周期公式的灵活运用情况.

　　解析：做自由落体运动，到C所需时间 ，R为圆弧轨道的半径．

　　因为圆弧轨道的半径R很大，B球离最低点C又很近，所以B球在轨道给它的支持力和重力的作用下沿圆弧作简谐运动（等同于摆长为R的单摆），则运动到最低点C所用的时间是单摆振动周期的 ，即 ，所以A球先到达C点．

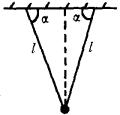　　例3：如图所示为一双线摆，它是在一水平天花板上用两根等长细线悬挂一小球而构成，每根摆线的长均为l，摆线与天花板之间的夹角为 ，当小球在垂直纸面的平面内做简谐运动时，其振动的周期是多少？

　　出题目的：此题主要考查振动周期公式中摆长的实际确定.

　　解析：双线摆可等效为摆长为 的单摆，利用单摆振动的周期公式得双线摆的周期为 。

　　例4：北京地区重力加速度 ，南京地区重力加速度 。在北京地区准确计时的摆钟搬到南京地区时，该钟是“走”快了还是“走”慢了？一昼夜相差几秒？应如何调节，该钟在南京地区才能准确计时？

　　出题目的：此题主要考查重力加速度对振动周期的影响情况.

　　解析：（1）该钟在北京和南京的摆动周期比

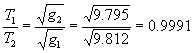
（或 ）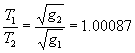

　　 ，在南京一天摆动的次数少了，所以“走”慢了。

　　（2）在北京计时准确，一昼夜摆动的次数为

　　该钟搬到南京时摆动周期为 ，摆动 次实际时间为 ，所以走时差为

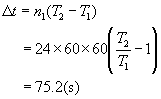
　　即一昼夜慢了75.2s。

　　（3）调整的办法是将摆长缩短一点，使 ，即

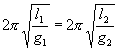
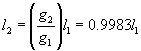
　　例5：如图，摆长为L的单摆，若在悬点O的正下方A点固定一颗钉子，A点距悬点O的距离为L／3，试求这个单摆完成一个全振动的时间是多少？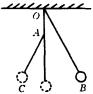

　　出题目的：此题主要考查振动周期公式的灵活使用情况.

　　解析：在摆角很小时，单摆的振动可视为简谐运动，当摆线不碰到钉子时，A点成为“悬点”，单摆的摆长由L变为2L／3。由题意知，

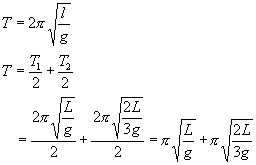
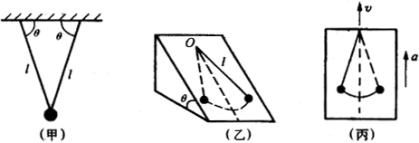
　　例6：试确定下列几个摆球在平衡位置附近来回振动的周期．

　　（1）如图（甲）所示．悬挂在水平横梁上的双线摆球．摆线长为l，摆线与水平横梁夹角 。

　　（2）如图（乙）所示．光滑斜面上的摆球．斜面倾角为 ，摆线长为l．

　　（3）如图（丙）所示．悬挂在升降机中的单摆，摆长为l，升降机以加速度a竖直向上做匀加速运动．

　　出题目的：本题主要考查等效摆长、等效重力加速度的实际运用情况.

　　解析：（1）双线摆在垂直于纸面的竖直面里作简谐运动，等效摆长为 ，故振动周期为

　　（2）摆球在光滑的斜面上来回振动，回复力由小球重力沿斜面向下的分力 决定，等效重力加速度为 ，其振动周期为

　　（3）升降机竖直向上作匀加速运动时，摆球“超重”，回复力由 决定，等效重力加速度为 ，摆球振动周期为

返回页首