 设为首页
设为首页
 加入收藏
加入收藏
典型例题(等容变化)
查理定律的应用
例1 电灯泡内充有氦氩混合气体,如果要使电灯泡内的混合气体在500℃时的压强不超过一个大气压,则在20℃的室温下充气,电灯泡内气体压强至多能充到多少?
解析:
解法1、由于电灯泡容积不变,故气体为等容变化,设500℃时压强为
![]() ,
, ![]() ℃时的压强为
℃时的压强为 ![]() ,0℃时的压强为
,0℃时的压强为 ![]() 。
。
![]()
![]()
![]()
解法2、由题意可知:
![]() ;
; ![]()
由查理定律: ![]() ∴
∴ ![]()
点拨:(1)
![]() 为0℃时气体的庆强.(2)处理一定质量的气体等容变化时的问题,用查理定律的两个表达式均可,要灵活运用,尽可能使问题简化.
为0℃时气体的庆强.(2)处理一定质量的气体等容变化时的问题,用查理定律的两个表达式均可,要灵活运用,尽可能使问题简化.
等容线
例2一定质量的气体,在压强不太大、温度不太低的情况下经历如图所示的一系列的过程,ab、bc、cd、da这四个过程在P-T图上都是直线段,其中ab的延长线通过坐标原点O,bc垂直于ab,而cd平行于ab,由图可以判断:
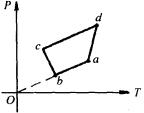 (A)ab过程中气体的体积不断减小
(A)ab过程中气体的体积不断减小
(B)bc过程中气体的体积不断减小
(C)cd过程中气体的体积木断增大
(D)da过程中气体的体积不断增大
解析:解此题需把握两方面的基础知识:第一,在图上只有过原点的直线才是等容线,本题ab的过程便是等容过程.第二,对于一定质量气体的等容线(过原点的直线),斜率越大,气体的体积越小,连接cO、dO,可以看到状态c的体积最小,状态d的体积大于状态c的体积,而小于状态a(或b)的体积.
本题正确答案为B、C、D
查理定律的适用条件
例3 如图所示的两条等容线,分别表示两个气缸中的一定质量的某种理想气体的等容变化规律;则两个体积的关系是:
 (A)
(A)
![]() (B)
(B) ![]()
(C)
![]() (D)无法确定
(D)无法确定
解析很多同学不加思索便会脱口而出: ![]() 应选B.
应选B.
其实,答案应选D.对于一定质量的同种气体,等容线的斜率和气体的体积有关.体积越大,斜率越小.但这两条等容线研究的对象分别为两个气缸中的质量不变的理想气体,根本不是同一对象,也没有告知两个对象间的质量关系和种类关系,因此正确答案只能是D.
点拨:在应用物理定律或规律时一定要注意它的适用条件.
关于等容变化的两种解法
例4 如图所示,两个容器中盛有质量相同的同种理想气体,用一段水平玻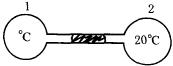 璃管将它们连接起来,在玻璃管的正中央有一段水银柱,当一个容器中的温度是0℃,另一个容器中的温度是20℃时,水银柱保持静止,如果将两容器中气体的温度都升高10℃,管中水银柱将向哪方移动?
璃管将它们连接起来,在玻璃管的正中央有一段水银柱,当一个容器中的温度是0℃,另一个容器中的温度是20℃时,水银柱保持静止,如果将两容器中气体的温度都升高10℃,管中水银柱将向哪方移动?
解析 这是一道讨论气体状态变化趋势的问题,解此类题的一般方法是:先弄清变化前的情况,再找出变化中的不变量,最后再找变化量及变化情况.
设左、右气体分别为气体1和气体2,变化前 ![]() .现在气体升温,水银柱若再移动,势必导致左、右气体三个状态参量均要变化,给问题的解决带来困难.先假设水银柱不动,先按等容情况讨论气体因温度升高而压强增大的情况,再看变化后的压强是否能保持平衡,若不能,则说明水银柱会移动,再根据压强的大小,判断水银柱将如何移动,下面介绍几种解法.
.现在气体升温,水银柱若再移动,势必导致左、右气体三个状态参量均要变化,给问题的解决带来困难.先假设水银柱不动,先按等容情况讨论气体因温度升高而压强增大的情况,再看变化后的压强是否能保持平衡,若不能,则说明水银柱会移动,再根据压强的大小,判断水银柱将如何移动,下面介绍几种解法.
解法1:设气体升温后左、右压强分别为
![]() 和
和 ![]()
据查理定律,对于左边气体, ![]()
对于右边气体, ![]()
又
![]()
![]()
∴
![]() 水银向右移.
水银向右移.
(此种方法对比较升高相同温度的题目比较方便,如果容器两边温度升高的不一样多,如左边升高5℃,右边升高10℃,那么 ![]() ,
, ![]() ,
, ![]() 、
、 ![]() 哪个大说不清楚)
哪个大说不清楚)
解法2:将左、右气体据查理定律分别写出
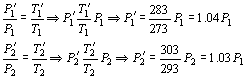
∴
![]() 向右移
向右移
解法3:
![]()
同理可知: ![]()
![]()
∴
![]()
解法4:图像法
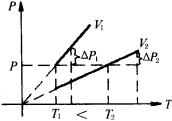
先假设水银不动,将状态变化看成等容变化过程.在P-T图像中分别画出两部分气体的等容图线,由于在压强P时, ![]() ,因此由图可知:
,因此由图可知: ![]() 表示左边气体,
表示左边气体, ![]() 表示右边气体.当温度升高
表示右边气体.当温度升高 ![]() 时,从图像可知;
时,从图像可知; ![]()
即:
![]()
思考:1.上题中若左、右气体同时降低10℃,问水银柱向哪方移动?(水银柱将向左方移动.请同学们依照以上四种解法加以证明)
2、上题中,若气体1和气体2开始时具有相同的温度,当两边气体升高或降低相同温度值时水银柱如何移动?(不移动,请同学自己证明)
两端封闭的玻璃管的等容变化
例5 两端封闭的玻璃管竖直放置,中间一段水银柱隔出两段气体,如图所示,这两段气体是![]() 质量相同的同种气体,且具有相同的温度.若使两段气体同时升高相同的温度,水银柱将如何移动?
质量相同的同种气体,且具有相同的温度.若使两段气体同时升高相同的温度,水银柱将如何移动?
解析本题同例4一样有多种解法,在此只用下列几种方法加以分析求解.
解法1:在温度升高前,1、2两气压强关系是
![]() ①
①
假设水银不动,据查理定律
对1气体:
![]() ②
②
对2气体:
![]() ③
③
联系①②③: ![]()
说明下段气体的压强增加得比上段气体快,于是水银将向上移动,下段气体体积增大
解法2:图像法
在P-T图像中分别画出两部分气体的等容线如图所示,
由于在温度T时, ![]() ,因此由图可知:
,因此由图可知: ![]() 表示上部分气体的体积,
表示上部分气体的体积, ![]() 表示下部分气体的体积.当温度升高
表示下部分气体的体积.当温度升高 ![]() 时,由图像可知:
时,由图像可知: ![]() ,即:
,即: ![]()
也就是:
![]()
所以水银柱上移
解法3:特殊值法
假设
![]() 则
则 ![]() 。温度升高到
。温度升高到 ![]() ,设
,设 ![]() ,据查理定律得:
,据查理定律得: ![]() ,显然
,显然 ![]() ,于是水银柱上移.
,于是水银柱上移.
思考:本例中若两部分气体的温度同时降低同一数值,水银柱将向哪一方移动?(向下移动,请同学们自己证明)
典型例题(等温变化)
玻意耳定律的应用
例1 如图所示,粗细均匀的U形玻璃管,右端开口,左端封闭,管内水银将一部分空气封闭在管中,开口朝上竖直放置时.被封闭的空气柱长24cm,两边水银面高度差为15cm,若大气压强为75cmHg柱高,问再向开口端倒入长为46cmHg柱时,封闭端空气柱长度将是多大?
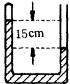
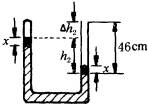
解析 取被水银封闭的那部分气体为研究对象.倒人水银前气体的体积和压强分别为 ![]() cmHg;倒cmHg;倒入水银后,左端水银面将上升,右端原水银面将下降.设左端水银面上升x,则由图得此时封闭气体长
cmHg;倒cmHg;倒入水银后,左端水银面将上升,右端原水银面将下降.设左端水银面上升x,则由图得此时封闭气体长
![]() 。
。
此时两边水银面高度差 ![]()
此时封闭气体的压强 ![]() cmHg
cmHg
据玻意耳定律 ![]() 得:
得: ![]() 解得:
解得: ![]() cm(舍去)
cm(舍去) ![]() cm(即所求)
cm(即所求)
关于水银的注入和吸出的等温变化
例2 如图所示,一端封闭的玻璃管总长为100cm,竖直放置,20cm高的水银柱封闭一段80cm长的气体,室温为27℃不变,大气压为76cmHg问:
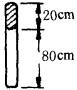 (1)能否继续向玻璃管内缓缓加入一些水银?
(1)能否继续向玻璃管内缓缓加入一些水银?
(2)用吸管缓缓从玻璃管中最多能吸出多少水银?
解析
据玻意耳定律 ![]() 由数学知识可知:当
由数学知识可知:当 ![]() 时,
时, ![]() 有极小值且大小等于
有极小值且大小等于 ![]() .此题气体初态为
.此题气体初态为 ![]() cm气柱,
cm气柱, ![]() cmHg
cmHg
故 ![]()
由
![]() ∴
∴ ![]() ∴
∴ ![]()
(1)当
![]() 时,
时, ![]() ,即压强改变量大于体积改变量.对初态而言,
,即压强改变量大于体积改变量.对初态而言, ![]() ,所以
,所以 ![]() ,即如加入水银,则压强的增大量大于体积的缩小量,即水银会溢出,所以不能继续向玻璃管内缓缓灌入一些水银.
,即如加入水银,则压强的增大量大于体积的缩小量,即水银会溢出,所以不能继续向玻璃管内缓缓灌入一些水银.
(2)反之,若抽出一些水银,则压强的缩小量大于气体体积增大量,即
![]() 之值减小,水银不会溢出,所以抽出一些水银是可以的.当抽到
之值减小,水银不会溢出,所以抽出一些水银是可以的.当抽到
![]() cmHg,
cmHg, ![]() cm长气柱时,
cm长气柱时,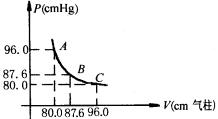 P、V之和最小,(如图中B点)再继续抽,则
P、V之和最小,(如图中B点)再继续抽,则
![]() 的值又要增大.由双曲线图像对称性(如图所示),当抽至
的值又要增大.由双曲线图像对称性(如图所示),当抽至
![]() cmHg,
cmHg, ![]() cm气柱长时,PV之和与初态相等,水银面与管口平齐(图中C点),再抽水银将自动溢出.
cm气柱长时,PV之和与初态相等,水银面与管口平齐(图中C点),再抽水银将自动溢出.
因此,从玻璃中最多吸出 ![]() cm长水银柱.
cm长水银柱.
点拨(1)注意
![]() 的值不是单调变化的.
的值不是单调变化的.
(2)本题还可用如下方法判断.
设可加管内加入水银xcm. ![]()
∴
![]()
![]() cm说明只能吸出16cm水银柱.
cm说明只能吸出16cm水银柱.
极限分析法分析等温变化
例3 一根一端封闭玻璃管开口向下插入水银槽中,内封一定质量的气体,管内水银面低于管外,在温度不变时稍向下插一些,下列说法正确的是,如图所示.
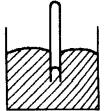 (A)玻璃管内气体体积减小
(A)玻璃管内气体体积减小
(B)玻璃管内气体体积增大
(C)管内外水银面的高度差减小
(D)管内外水银面的高度差增大
解析
设想把管压下很深,则易知V减小,P增大,
![]() ,∴h增大.即A、D正确.
,∴h增大.即A、D正确.
点拨(1)上述分析方法为极限分析法即:把某变化条件合理外推到区间的两端,由物理概念或规律将矛盾迅速暴露出来,此方法对定性处理选择题填空题中增大、减小、向左、向右等问题时特别方便.但对先增后减或先减后增的情况不适用.
(2)“合理外推”指不违背物理概念、规律的约束,应在题设物理情景、条件变化范围内外推.
抽气机的有关等容变化
例4
一容器的体积为
![]() ,封在容器中的气体的压强为
,封在容器中的气体的压强为 ![]() ,现用活塞式抽气机对容器抽气,活塞筒的有效抽气容积为V,其工作示意图如图所示,
,现用活塞式抽气机对容器抽气,活塞筒的有效抽气容积为V,其工作示意图如图所示,
![]() 为工作阀门.求抽气机抽n次后容器里
为工作阀门.求抽气机抽n次后容器里 气体的压强(设温度不变).
气体的压强(设温度不变).
解析
抽气容器中的空气等温膨胀,体积由 ![]() 变成
变成 ![]() ,压强逐渐减小,据玻意耳定律
,压强逐渐减小,据玻意耳定律
第一次抽
![]()
![]()
第二次抽
![]()
![]()
推理可知,第n次抽气后, ![]()
点拨 解这类题的思路是研究抽1次、2次结果后,推理出抽n次的情况.
关于活塞与气缸的两种研究方法
例5 如图所示,气缸筒的质量为M,活塞(连同手柄)的质量为m.气缸内部的横截面积为S,大气压强为 ![]() ,平衡时气缸内的容积为V,现用手握住活塞手柄缓慢向上提,设气缸足够长,在整个上提过程中气体温度保持不变,并且不计气缸内气体重力及活塞与气缸间的摩擦,求将气缸刚提离地面时活塞上升的距离.
,平衡时气缸内的容积为V,现用手握住活塞手柄缓慢向上提,设气缸足够长,在整个上提过程中气体温度保持不变,并且不计气缸内气体重力及活塞与气缸间的摩擦,求将气缸刚提离地面时活塞上升的距离.
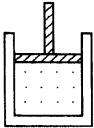
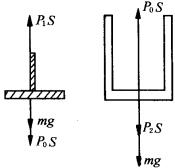
解析取被封闭的气体为研究对象
初态(气缸未被提时) ![]()
末态(刚提气缸离地),设活塞上升距离为x, ![]()
对气缸受力如图所示, ![]() ∴
∴ ![]()
由
![]() 得:
得: ![]()
解得:
![]()