第二节 法拉第电磁感应定律--感应电动势的大小

典型例题

关于平均感应电动势与瞬时感应电动势

　　例1 如下图所示，长为L的铜杆OA以O为轴在垂直于匀强磁场的平面内以角速度 匀速转动，磁场的磁感应强度为B，求杆OA两端的电势差．

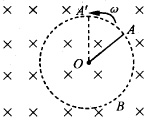
　　分析：铜杆OA在匀强磁场中做切割磁感线运动，将产生感应电动势E，此即OA杆两端的电势差．

　　解：OA杆匀速转动时，杆上各点运转半径不同，线速度大小不同，由 知线速度v与半径r成正比，可见感应电动势从A至O是逐段均匀减小的，能够用平均值来计算OA杆的感应电动势．

　　杆的平均速度

　　感应电动势

　　杆OA两端的电势差

点评：本题亦可用法拉第电磁感应定律求解

　　设杆OA经过时间 ，从OA位置转至 位置，杆扫过的扇形面积为

　　此面积对应的磁通量变化量为

　　所以，感应电动势平均值

　　由于OA杆在任意时刻产生的感应电动势都相同，且 位置为任取的，可见，平均感应电动势也就是每个时刻的瞬时感应电动势，因此，杆OA两端电势差

关于感应电动势的平均值

　　例2 如下图所示，半径为r的金属环绕通过某直径的轴 以角速度 作匀速转动，匀强磁场的磁感应强度为B，从金属环面与磁场方向重合时开始计时，则在金属环转过30°角的过程中，环中产生的电动势的平均值是多大？

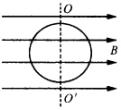
　　分析：根据金属环在磁场中转动的始末位置穿过环的磁通量 和 以及完成这一变化所用时间 ，就可以求出环中产生的感应电动势 ．

　　解：当金属环面与磁感线平行时，穿过环的磁通量 ．当环转过对30°时，环平面在垂直磁感线方向的投影 ，穿过环的磁通量 ．所以，在环转过30°的过程中，环中平均感应电动势 ．

关于感应电动势大小的求解

　　例3 如图1所示把线框abcd从磁感应强度为 的匀强磁场中匀速拉出，速度方向与ab边垂直向右，速度的大小为 ，线圈的边长为 ，每边的电阻为 ，问，线圈在运动过程中，ab两点的电势差为多少？

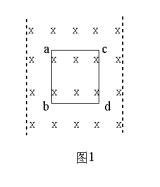
分析：

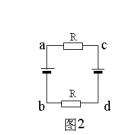
　　当线框abcd 整个在磁场的时候，穿过线圈的磁通量不变，无感应电流，ab和cd两边切割磁感线，等效电路图如图2所示：



　　当cd边离开磁场，ab边切割磁感线，ad，bc，cd边的电阻属于外阻，等效电路图如图3所示：



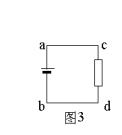
　　解：当线框abcd 整个在磁场的时候：

　　当cd 边离开磁场的时候：

关于感应电动势求解公式的简单应用

　　例4　在边长为a的等边三角形的区域内有匀强磁场 ，其方向垂直纸面向里，一个边长也为a的等边三角形导线框EFG正好与上述磁场区域边界重合，尔后以周期 绕几何中心O在纸面内匀速转动，于是框架EFG中产生感应电动势，经过 线框转到图中虚线位置，则在 内，线框的平均感应电动势的大小为多少？

分析：

　　在求平均感应电动势的题目中，应该首先想到用法拉第电磁感应定律 求解，公式中涉及到磁通量 的变化，在高中阶段主要涉及到两种情况，一是回路与磁场垂直的面积不变，磁感应强度发生变化，二是磁感应强度不变，而线圈与磁场垂直的面积发生变化．

　　本题属于第二种情况，那么应该利用公式： 求解．

　　解：

返回页首