 设为首页
设为首页
 加入收藏
加入收藏
例1 一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g.用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才平衡?若秤杆长60cm,则这把秤最大能称量多少千克的物体?(如图13-1-9所示)
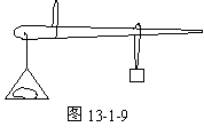
选题目的:训练学生用杠杆平衡条件解决实际生活问题的能力,提高分析解题能力.
分析:杆秤也是一个杠杆.提纽处看作杠杆支点.若将重物对杆的力看作动力F1,物体离提纽的距离就是动力臂l1;则秤砣对杆的力就是阻力F2,秤砣离提纽的距离是阻力臂l2.(如图13-1-10所示)

已知: m1=2kg,m2=0.25kg,l1=4cm,l2 '=60 cm -4 cm =56 cm
求:l2=?m1 '=?
解:由于物体和秤砣对杠杆的力分别等于各自的重力,
根据杠杆平衡条件:F1L1=F2L2,
得 m1g l1 = m2g l2
2kg×g ×4cm = 0.25kg ×g×l2
l2=32cm
即称2kg物体时秤砣离提纽32cm.
当阻力臂最大时,称量物体质量最大.l2 '=56cm
由F'1'l1=F2 l'2,得m1'g l1 = m2g l2'
m1'×g×4cm = 0.25kg×g×56cm
m1'=3.5 kg
即秤的最大称量是3.5kg.
答:称2kg物体时秤砣离提纽32cm,秤的最大称量是3.5kg.
例2 一根长为18 cm的木棒,两端分别挂着5N和10N的重物,要使木棒在水平位置上平衡,需在何处作支点?若平衡后两端各增挂5N的重物,分析说明木棒是否还平衡?
选题目的:教会学生利用杠杆平衡条件解决问题,提高分析能力.
分析:在利用杠杆平衡条件解决问题时,一般先画出杠杆受力示意图,确定好对应的力和力臂,以免出现如动力与阻力臂相乘的错误.本题受力示意图见图13-1-8.
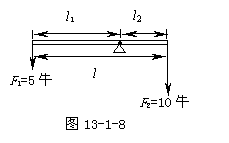
已知:l=18 cm,F1=5N,F2=10N
求:l1;分析平衡后两端各增挂5N的重物是否还能平衡?
解:根据杠杆平衡条件:F1l1=F2l2
各力臂和杆总长的关系:l=l1+l2
5N×l1=10N×(18 cm -l1)
l1=12 cm,即支点应位于力F1作用点右侧12cm处.
若两端个增加5N的重物,则F1'=10N, F2'=15N
影响杠杆转动的因素是力与力臂的乘积,所以
杠杆左侧使杠杆逆时针转动的F1'l1=10N'×12cm =120N·cm
杠杆右侧使杠杆逆时针转动的F2'l2=15N'×(18cm -12cm)
由于120N·cm>90N·cm
杠杆将不平衡,将逆时针转动.
答:支点距挂5牛重物一端12cm,若两端各增加5N重物,杠杆将不平衡,原来挂5牛重物一端下沉.
例3 .如图13-1-6所示是用道钉撬撬起道钉的示意图,请画出作用在道钉撬上动力F1的力臂.
选题目的:教会学生规范画图,训练学生的作图能力.
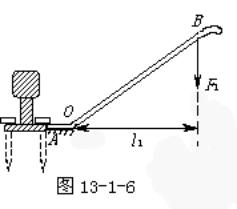
分析与解答 力臂是从支点到力的作用线的距离.画力臂是重要的作图之一,要注意作图规范.画力臂可以从以下几步进行:
辨认杠杆,确定支点;将力的作用线用虚线延长(有时可不用延长);从支点向力的作用线作垂线,标垂足,垂线要用虚线;力臂用双向箭头(或大括号)表示出,在旁边标上字母l.
本题作图如图13-1-7所示.
