 设为首页
设为首页
 加入收藏
加入收藏
典型例题
例1 计算
(1)(-9)+(-8); (2) ![]() ;
;
(3) ![]() ; (4)
; (4) ![]() 。
。
解(1)(-9)+(-8)=-(9+8)=-17
(2) ![]()
![]()
![]() ;
;
(3) ![]()
![]()
(4) ![]()
![]() 。
。
说明:(1)在有理数加法运算时,应注意包括符号确定和绝对值运算两部分。绝对值计算是小学数学中的计算,而符号又分为同号两数与异号两数两种情况。因此计算时应先确定和的符号,再计算它们的绝对值。
(2)注意特殊情况:一个数与0相加仍得这个数;互为相反数的两个数相加得0。
(3)第(2)题的结果中“ ![]() ”要注意约分。
”要注意约分。
例2 计算 ![]()
分析 做带分数加法时,可将整数部分与分数部分相加,然后再把结果相加;但要注意:①分开的整数部分与分数部分必须保持原带分数的符号。②运算符号和数的性质符号要用括号分开,如:
![]() ,这里的“+”是运算符号,“-”是性质符号,这两个符号不能连在一起写成“
,这里的“+”是运算符号,“-”是性质符号,这两个符号不能连在一起写成“
![]() ”。
”。
解 ![]()

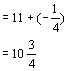
例3 计算:
(1)16.96+(-3.8)+5.2+(-0.2)+(-0.96)
(2) ![]()
分析:(1)中16.96+(-0.96)和(-3.8)+(-0.2)都是整数,应当先做加法;
(2)中分母为37的分数分布在两个中括号里,应当先去掉中括号,运用加法的交换律和结合律,把分母为37的分数结合起来运算,才能使计算简便.
解:(1)原式=[16.96 + (-0.96)] + [(-3.8) + (-0.2)] + 5.2
=16+(-4)+5.2
=17.2
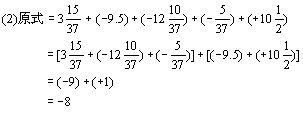
说明:学会观察是此例训练的目的,对于较为复杂的题,先观察分析,发现加数间的联系,而后再选择一个最佳方案,是解决问题的一般思路.在数学的学习中,有意识地培养这种能力是非常重要的,多个有理数相加时,应灵活运用加法运算律,适当交换各个加数的位置,遇到分数,先把同分母的分数结合;遇到小数,先把相加得整数的小数结合.这样能使计算简便些.
例4 某产粮专业户出售余粮20袋,每袋重量如下:(单位千克)
199、201、197、203、200、195、197、199、202、196、
203、198、201、200、197、196、204、199、201、198.
用简便方法计算出售的余粮总共多少千克?
分析:把这20个数逐一相加是很麻烦的,而且容易出错,注意到,这20个数都在200(千克)左右,若以200为准,超过的千克数记作正数,不足的千克数记作负数,那么通过计算差额来求总和则简便得多.
解:以200(千克)为基准,超过的千克数记作正数,不足的千克数记作负数,则这20个数的差的累计是:
(-1)+(+1)+(-3)+(+3)+0+(-5)+(-3)+(-1)+(+2)+(-4)+(+3)+(-2)+(+1)+0+(-3)+(-4)+(+4)+(-1)+(+1)+(-2)
=(-5)+(-4)+(-3)+(-2)
=-14
200×20+(-14)=4000-14=3986(千克)
答:出售的余粮共3986千克.
说明:例4的解题方法叫做“基本数求和法”,是数据比较多且都在某基本数附近时求它们和的简便方法.其中200(千克)叫做基本数,20(袋)叫做项数,求和的计算公式是:
总和=基本数×项数+累计差