 设为首页
设为首页
 加入收藏
加入收藏
典型例题
例1 计算
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() .
.
分析:在应用乘法公式进行实际问题的计算时,多项式的系数、指数、符号、相对位置不一定符合公式的标准形式,但只要对题目的结构特征进行认真观察,就可以发现这几个题目都可以应用平方差公式进行计算.
解 (1)原式![]()
![]()
(2)原式![]()

或原式![]()
![]()
![]()
(3)原式![]()
![]()
(4)原式![]()
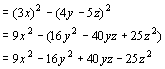
说明:1)乘法公式中的字母![]() ,可以表示数,也可以表示字母,还可以表示一个单项式或多项式;2)适当添加括号,将有利于应用乘法公式,添加括号的方法不同,一题可用多种解法,得出相同的结果;3)一定要认真仔细地对题目进行观察研究,把不符合公式标准形式的题目,加以调整,使它变化为符合公式标准的形式.
,可以表示数,也可以表示字母,还可以表示一个单项式或多项式;2)适当添加括号,将有利于应用乘法公式,添加括号的方法不同,一题可用多种解法,得出相同的结果;3)一定要认真仔细地对题目进行观察研究,把不符合公式标准形式的题目,加以调整,使它变化为符合公式标准的形式.
例2 计算:
(1)![]()
(2)![]()
分析:(1)中的![]() 都可以利用平方差公式计算,
都可以利用平方差公式计算,![]() 可以利用多项式乘法法则计算.
可以利用多项式乘法法则计算.
(2)中的![]() 可以逆用幂的运算法则,写成
可以逆用幂的运算法则,写成![]() 再计算.
再计算.
解:(1)原式![]()
![]()
(2)原式![]()

说明:(1)平方差公式积适用于![]() 类型的多项式乘法,其中
类型的多项式乘法,其中![]() 、
、![]() 可以是数,也可以是单项式或多项式.
可以是数,也可以是单项式或多项式.
(2)逆用幂的运算法则,![]() 是常用的解题技巧.
是常用的解题技巧.
(3)此题中的第(1)题先利用乘法的交换律及结合律合理变形后,可连续运用平方差公式;第(2)题先利用加法结合律,把两个因式变为“两数的和与这两数的差”的形式,进而利用平方差公式计算.这些都是常用的解题技巧.