第三节 分组分解法

典型例题

　　例1（1） ；（2）

　　解：（1）

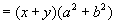
或

；

　　（2）

或

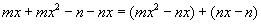
　　说明：（1）把有公因式的各项归为一组，并使组之间产生新的公因式，这是正确分组的关键所在。因此，分组分解因式要有预见性；

　　（2）分组的方法不唯一，而合理的选择分组方案，会使分解过程简单；

　　（3）分组时要用到添括号法则，注意在添加带有负号的括号时，括号内每项的符号都要改变；

　　（4）实际上，分组只是为实际分解创造了条件，并没有直接达到分解的目的。

　　例2把下列各式分解因式：

　　（1） ；（2） ；

　　（3）

　　解：（1）

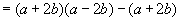
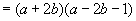
　　（2）

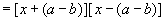
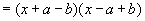
　　（3）

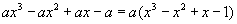
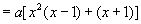
或

或

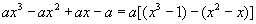
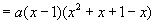
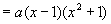
　　说明：（1）要善于观察多项式中存在的公式形式，以便恰当地分组；同时还要注意统观全局，不要一看到局部中有公式形式就匆匆分组。如，

，就会分解不下去了；

　　（2）有公因式时，“首先考虑提取公因式”是因式分解中始终不变的原则，在这里，当提取公因式后更便于观察分组情况，预测结果；

　　（3）对于一道题中的多种分组方法，要善于选择使分解过程简单的分组方法，如题中前两种分组显然优于后者。

　　例3把下列各式分解因式

　　（1） ；（2） .

　　分析（1） 的二次项系数是1，常数项 = ，一次项系数= ，故这是一个 型式子。

　　（2） 的二次项系数是1，常数项 = ，一次项系数 ，故这也是一个 型式子。

　　解：(1) = .

　　(2) = .

　　说明：因式分解时常数项因数分解的一般规律：

　　(1)常数项是正数时，它分解成两个同号因数，它们和一次项系数符号相同.

　　(2)常数项是负数时,它分解成两个异号因数,其中绝对值较大的因数和一次项系数的符号相同.

　　例4将 分解因式

　　分析：此例不能直接用提公因式法或运用公式法分解因式，用分组分解法又不具备运用分组分解法的题目特点，而用 型式子分解因式其二次项系数不是1，而是 ，故在上述都不能的情况下，想方法将 看成 ，则这个二次三项式就可以化成 ，即可符合 型式子，故可分解因式.

　　解：设 ，则原式=

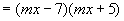
所以， .

　　说明：今后应细心审题观察题目的特征，若能利用整体换元的思想将多项式化为 型的式子即可因式分解。

返回页首