第十一节 作图题举例

典型例题

　　例1 、求作等腰直角三角形，使它的斜边等于已知线段

　　已知：线段

　　求作： ，使∠A＝90°，AB＝AC，BC＝

　　分析：由于等腰直角三角形比较特殊，内角依次为45°， 45°， 90°，故有如下几种作法：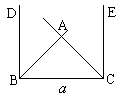

　　作法一：1、作线段BC＝

　　2、分别过点B、C作BD、CE垂直于BC

　　3、分别作∠DBC、∠ECB的平分线，交于A点

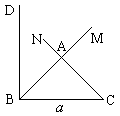　　 即为所求

　　作法二：作线段BC＝

　　2、作∠MBC＝45°

　　3、作∠NCB＝∠MBC，CN与BM交于A点

　　 即为所求

　　作法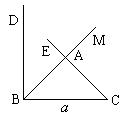三：1、作线段BC＝

　　2、作∠MBC＝45°

　　3、过C作CE⊥BM于A

　　 即为所求

　　作法四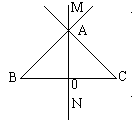：1、作线段BC＝

　　2、作BC的中垂线，交BC于O点

　　3、在OM上截取OA＝OB，连结AB，AC

　　 即为所求

　　说明：几种作法中都是以五种基本作图为基础，

　　不要求写出基本作图的作法和证明。

　　例2、已知三角形的两边和其中一边上的中线长，求作这个三角形.

　　已知：线段a、b为两边，m为边长b的中线

　　求作： ，使BC=a，AC=b，且AM=MC，BM=m.

　　分析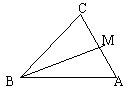：先画草图，假定 为所求的三角形，则有BC=a，AC=b，设M为AC边的中点，则MB=m,而 ，故 的三边为已知作出，然后再作出 .

　　作法：（1）作 ，使BC=a， ，MB=m；

　　（2）延长线段CM至A，使MA=CM;

　　（3）连接BA，则 为所求作的三角形.

　　小结：本题的突破口是找 与所求的 的关系.由于 的三边已知，故 即可顺利作出.

　　例3、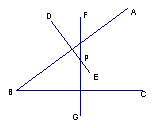如图，A、B、C三点表示三个村庄，为解决村民就近入学问题，计划新建一所小学，要使学校到这三个村庄的距离相等，请你在图中用尺规确定学校的位置P.

　　分析：分两步：先作到A、B两点距离相等的点的图形，再作到B、C两点等距离的点的图形，两图形的交点，这就是所求作的点.

　　作法：（1）连结AB，做线段AB的垂直平分线DE；

　　（2）连结BC，作线段BC的垂直平分线FG，交DE与点P.

　　则点P为所求作的学校位置.

　　小结：由于不能直接确定到三点距离相等的点的位置，可以分解为先求到A，B相等的所有点，再求作到B，C相等的所有点，交点即所求.

返回页首