第四节 最简二次根式

典型例题

　　1． 关于最简二次根式概念的例题

　　例1 下列二次根式中哪些是最简二次根式？哪些不是？为什么？

　　

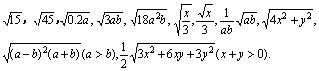
　　分析： 判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式的定义进行，或直观地观察被开方数的每一个因数(或因式)的指数都小于根指数2，且被开方数中不含有分母，被开方数是多项式时要先因式分解后再观察。

　　解： 最简二次根式有：

　　

　　其余的均不是最简二次根式，因为

　　　

　　　

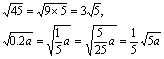
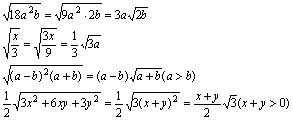
　　说明： 最简二次根式必须同时满足下列两个条件：

　　(1)被开方数的因数是整数，因式是整式；

　　(2)被开方数中不含有能开得尽方的因式或因数(被开方数不含平方因子)。

　　 2． 关于把二次根式化为最简二次根式的例题

　　例1　把下列二次根式化为最简二次根式

　　

　　分析：化简二次根式的过程，一般按以下步骤：把根号下的带分数或绝对值大于1的小数化成假分数，把绝对值小于1的小数化成分数；被开方数是多项式的要因式分解；使被开放数不含分母；将被开方数中能开的尽方的因数或因式用它的算术平方根代替后移到根号外面；化去分母中的根号；约分．本例题中的2道题都是基础题，只要将被开方数中能开的尽方的因数或因式用它的算术平方根代替后移到根号外面即可．

　　解：

　　　

　　说明：最简二次根式必须同时满足下列两个条件：

　　（1）被开方数的因数是整数，因式是整式；

　　（2）被开方数中不含有能开得尽的因式或因数（被开方数不含平方因子）．

　　说得再通俗些，根号里没有分母，分母里没根号，能开的全开出来．

　　例2　把下列二次根式化为最简二次根式

　　

　　分析：化简二次根式的过程，一般按以下步骤：把根号下的带分数或绝对值大于1的小数化成假分数，把绝对值小于1的小数化成分数；被开方数是多项式的要因式分解；使被开放数不含分母；将被开方数中能开的尽方的因数或因式用它的算术平方根代替后移到根号外面；化去分母中的根号；约分．本例题中的2道题被开方数都是多项式，应先进行因式分解．

　　解：

　　　

　　　

　　说明：被开方数中能开的尽方的因数或因式的算术平方根移到根号外面后要注意符号问题．

　　例3　把下列二次根式化为最简二次根式

　　

　　分析：根号下的带分数应化成假分数．

　　解：

　　　

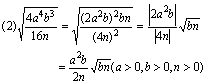
　　说明：当然(2)题也可以如下处理：

　　

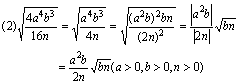
　　例4　把下列二次根式化为最简二次根式

　　

　　分析：被开方式比较复杂时，要先对被开方式进行处理。

　　解：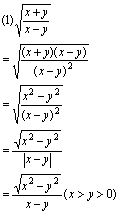　　

　　　　

　　说明：运算中要注意运算的准确性和合理性．

　　例5　把下列二次根式化为最简二次根式

　　

　　说明：比较复杂的被开方式先处理一下会简单些．

　　解：　　

返回页首