第八节 由一个二次方程和一个可以分解为两个二元一次方程组成的方程组

典型例题

　　例1  用两种不同的方法解方程组

　　

　　解法1  由（1）得  　（3）

　　（3）代入（2）中，得

　　，

　　即　　。

　　解之，得　　

　　代入（3）中，得　　。

　　∴　原方程组的解是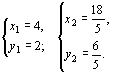

　　解法2  由（2）得，

　　∴　或。

　　∴　原方程组可化为两个二元一次方程组

　　

　　∴　原方程组的解是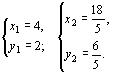

　　评注：解法1是代入消元法，具体思维过程是：先消元，再把原方程组转化为一元二次方程；解法2是分解因式法，具体思维过程是：先降次，再把原方程组转化为两个二元一次方程组。两种解法，各有千秋，但都体现了一种共同的数学思想——化归思想，即把新问题转化归结为我们已知的问题。

　　例2  解方程组：

　　

　　分析：一些含有、、的二元二次方程组，除可以且代入法来解外，往往还可以利用根与系数的关系，将解二元二次方程组化为解一元二次方程的问题。有时，后者显得更为简便。

　　

　　解法1  由（1）得  ，　（3）

　　由（3）代入（2），整理，得

　　。

　　解得　　。

　　把分别代入（3），得

　　。

　　∴　原方程组的解是

　　解法2  把、看作一元二次方程的根

　　解得  。

　　∴　原方程组的解是

　　

　　解法1  由（2）得：。　（3）

　　把（3）代入（1），整理，得

　　

　　解得  。

　　把分别代入（3），得

　　。

　　∴　原方程组的解是

　　解法2  把（2）式左右两边平方得：

　　，　　（3）

　　（3）－（1）得，

　　即 

　　把x、y看作方程的根，

　　解得　。

　　∴　原方程组的解是

　　评注：显然，此处（1）、（2）题中解法二都比解法一快捷、简便，但要求能较好地理解一元二次方程根与系数的关系及熟练掌握、、、之间的运算关系。

　　例3  为何值时，方程组

　　

　　有两个不同的实数解？有两个相同的实数解？

　　分析：将一次方程代入二次方程，将之化为关于的一元二次方程来解之。

　　解：

　　由（2），得

　　（3）

　　将（3）代入（1），得

　　

　　即  ，　（4）

　　

　　∵  当，即，即或时，方程（4）有两个不相等的实根，所以方程组有两组不同的实数解。

　　因为当，即，即时，方程（4）有两个相等的实根，所以方程组有两组相同的实数解。

　　评注：方程组相同的实数解，应看作一组解。

　　例4  k为何值时，方程组

　　（1）有两组不相等的实数解；（2）有相等实数解；（3）无实数解。

　　分析：方程组的解的情况取决于消元后一元二次方程的根的情况。因此应先消元，再根据一元二次方程根的判别式来确定k的取值。

　　解：把（2）代入（1），整理，得

　　，   （3）

　　  时，（3）式为一元二次方程，

　　    。

　　（1）当时，方程组有两组不等实数解，

　　解得  且时，方程组有两组不相等的实数解。

　　（2）当时，方程组有相等实数解，

　　解得时，方程组有两相等实数解。

　　（3）当时，方程组无实数解，

　　解得时，方程组无实数解。

　　例6  A、B两地间的路程为36千米。甲从A地，乙从B地同时出发相向而行，两人相遇后，甲再走2小时30分到达B地，乙再走1小时36分到达A地，求两人的速度。

　　解：设甲、乙的速度分别为x千米/时，y千米/时，根据题意，得

　　

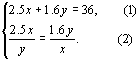
　　解方程组，得

　　

　　答：略。

　　评注：（2）式实际上是一个二元二次方程，即。

返回页首