第一节 正弦和余弦

典型例题

　　例1：在 中， ，求 的值。

　　分析：利用余弦函数的定义求解。

　　解：如图，在 中， ∴不妨设 ，由勾股定理可求，     为所求。

　　说明：已知锐角 的一个三角函数值，求角 的其余三角函数值，这类题目应熟练掌握。同时注意数形结合在题目中的应用，还可以让学生思考：此题是否有其他的解法？

　　例3：如图， 中， ，BC= ，AC=3，求 的值。

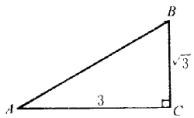
　　分析：本题综合考查勾股定理，正弦、余弦的定义和代数式的运算。即先用勾股定理求出第三边，然后根据锐角正弦、余弦的定义去求得。

　　解：由勾股定理得：

　　

　　 ，

　　 ，

　　 。

　　

　　

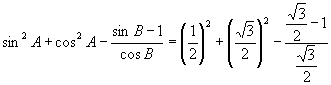
　　说明：应先把边求出，再求锐角的正、余弦值，最后代入化简，当然若要求出A、B的度数，也是可以的，本例实际上 ， 。

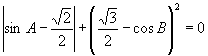　　例4 ，在 中，若 ， ， 都是锐角，则 的度数是（ ）

　　（A） 　（B） 　（C） 　（D）

　　分析：此例是非负数的性质结合正、余弦函数知识应用的问题。在 中，要求 的度数，应先确定 、 的度数。

　　解：

　　     ，

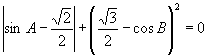
　　即 ， 。

　　又 ， ，

　　 ， ，

　　 ，

　　 ，故应选（C）。

　　说明：已知锐角 的三角函数值，求角 的值，这类题目也应熟练掌握，此类题目能很好的训练学生的逆向思维，同时也是以后高中学习解三角方程的基础。

　　例5 在 中，求证： 。

　　分析：要想证明 成立，只要证明 与 互余即可，而要证明 + = ，则要借助于三角形的内角和定理。

　　解：在 中，

　　

　　

　　

　　 。

　　说明：等式 成立是有条件的，即“在 中”如果把这个条件去掉，则等式就不一定成立了。类似地还可以证明 。

　　例6 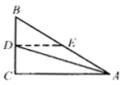如图，已知 中， ，AD是角平分线，且 ，求 的值。

　　分析：要求 ，由定义只要求 即可，但有困难，可考虑过D作AC的平行线交AB于点E，得Rt ，求出 ，即可。

　　解：作 交AB于点E。

　　则 。

　　 ，

　　 。

　　 。

　　 ， ，

　　 ，在 中， 。

　　 。

　　例7：在 ， ，斜边 ，两直角边的长 是关于 的一元二次方程 的两个根，求 较小锐角的正弦值。（2002年北京市东城区中考试题）

　　解： 是方程 的两个根，

　　 ，

　　在 ，由勾股定理得

　　而 ， ，

　　

　　即

　　解关于 的方程，得 ，

　　 是 的两条直角边的长，

　　

　　因此 不合题意，舍去。

　　

　　当 时，原方程为

　　解这个方程，得 ， 。

　　不妨设 ，则

　　 较小锐角的正弦值为 。

返回页首