 设为首页
设为首页
 加入收藏
加入收藏
典型例题
【例4】 某灯塔B在观测点A的北30°的方向,船M在灯塔正东方向,且在观测点A的北60°东的方向距A30海里,求若船M在上午11点10分出发,下午1点40分时驶抵灯塔B处,求船的速度(精确到0.1海里).

分析 只需延长MB,归结为解直角三角形问题来加以解决.
解:延长MB和正北的方向线相交于C,得![]() .在
.在![]() 中,有
中,有![]() ,所以
,所以
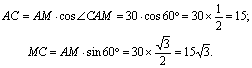
又,在![]() 中,
中,![]() ,所以
,所以
![]() .
.
于是,有
![]() .
.
据题意,船M行驶到B只用时2.5小时,所以,船的速度为
 (海里/时)
(海里/时)
答:这艘船的速度是6.9海里/时.
点拨 由于南北方向线和东西方向线互相垂直.所以航海问题大都能归结为解直角三角形问题;本例由于所给的已知角都是特殊角,所以也可用平面几何图形的性质和勾股定理来解.如设![]() (海里),证
(海里),证

于是,根据勾股定理,有

由于![]() ,所以得
,所以得
![]() .
.
下同.
【例5】 某水坝的断面是梯形,上宽![]() (米),底角
(米),底角![]() ,坡BC的坡比
,坡BC的坡比![]() ,坝高为20米,求坝底的宽(精确到0.1米).
,坝高为20米,求坝底的宽(精确到0.1米).

分析 分别解![]() .
.
解:在![]() 中,有
中,有
![]() ;
;
在![]() 中,有
中,有
![]()
∴![]()
又,![]() ,所以
,所以
![]() (米)
(米)
答:坝底宽约为41.5米.
【例6】 在距山坡脚B100米的测点A测山顶上高压输电铁塔顶端M的仰角为![]() ,测底端N的仰角为
,测底端N的仰角为![]() ,求铁塔的高(精确到0.1米,如图).
,求铁塔的高(精确到0.1米,如图).

分析 ![]() 和
和![]() 都是直角三角形,且
都是直角三角形,且![]() .
.
解:在![]() 中,有
中,有
![]() ,
,
在![]() 中,有
中,有
![]()
所以,铁塔的高度为
![]() (米)
(米)
点拨 应当注意,![]() 不是视线和水平线的夹角,所以它既不是仰角,也不是俯角.
不是视线和水平线的夹角,所以它既不是仰角,也不是俯角.
【例7】 某直升飞机在我迫击炮阵地M上方测得敌军雷达站P的俯角为15°,在向点P的迎面沿仰角30°的方向飞行,升高100米后再测点P的俯角为30°,分别求原飞行高度和点M到点P的水平距离(![]() ).
).
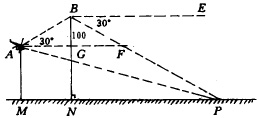
分析 据题意,画出图形.如图,仰角![]() ,俯角
,俯角![]() (m).
(m).
解![]() 可得AG的长.由于
可得AG的长.由于![]() 和
和![]() 都没有已知的边长所以都不能独立解出,所以应列方程组求解.
都没有已知的边长所以都不能独立解出,所以应列方程组求解.
解:在![]() 中,
中,![]() ,所以
,所以
![]() ,
,
设![]() ,于是分别在
,于是分别在![]() 和
和![]() 中,有
中,有
![]()
消去y,整理,得

把![]() 代入②,得
代入②,得
![]() ,
,
于是,有
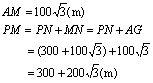
答:我直升机的原飞行高度为![]() 米,炮兵阵地M到P的距离为(
米,炮兵阵地M到P的距离为(![]() )米.
)米.
点拨 在解题时,首先要准确画图,理解题意,确定可解的直角三角形.如果没有直接可解的三角形,不能用一元方程求解,则应考虑到方程组求解.