第二节 过三点的圆

典型例题

　　例1、如图，表示一块破碎的圆形木盖，确定它的圆心．

　　分析：根据“不在同一直线上的三点确定一个圆”的原理可作出圆心．

　　作法：(1)在弧上任取三点A、B、C；

　　(2)连接AC、BC；

　　(3)分别作AC、BC的中垂线MN、PQ，相交于点0，点0即为所求圆心．

　　说明：此题是最基础的题目，主要培养学生的作图能力，学生必须落实.

　　例2、如图，在△ABC中，BD、CE为△ABC的中线，延长BD到F，使DF=BD.延长CE到G，EG=CE.求证：过A、G、F三点不能作圆．

　　分析：只要证明点G、A、F三点共线即可．

　　证明：连接AG、AF、BG、CF.

　　∵AD=DC、BD=DF，

　　∴四边形ABCF是平行四边形．故AF∥BC.

　　 同理AGBC是平行四边形，故AG∥BC.

　　∴点G、A、F三点在同一直线上．

　　∴过点G、A、F不可能作圆．

　　说明：此题是小型一个综合题，主要培养学生的思维能力.

　　例3、如图，在梯形ABCD中，AB∥CD，E、F分别是AD、BC的中点，连结EF．

　　求证：EF∥AB

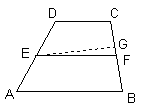
　　分析：对反证法思想的理解和基本步骤的掌握是解决本题的关键.

　　证明：(用反证法证明)

　　假设EF与AB不平行，作EG∥AB交BC于G(如图所示)，

　　则

　　∵E为AD的中点，∴CG＝BG即G是BC的中点

　　∵一条线段只有一个中点，∴F不是BC的中点，这与已知条件矛盾

　　因此假设EF与AB不平行是错误的，∴EF∥AB

　　说明：此题目的是理解和掌握反证法的基本步骤，是初中应用反证法证明的典例之一.

　　例4、用反证法证明：等腰三角形的底角必定是锐角．

　　分析：解题的关键是反证法的第一步否定结论，需要分类讨论.

　　已知：在△ABC中，AB=AC.求证：∠A、∠B为锐角.

　　证明：假设等腰三角形的底角不是锐角，那么只有两种情况：

　　(1)两个底角都是直角；  (2)两个底角都是钝角；

　　(1)由∠A=∠B=90°则∠A+∠B+∠C=∠A+90°+90°>180°，这与三角形内角和定理矛盾，∴∠A=∠B=90°这个假设不成立.

　　(2)由90°＜∠B＜180°，90°＜∠C＜180°，则∠A+∠B+∠C>180°，这与三角形内角和定理矛盾.∴两个底角都是钝角这个假设也不成立．

　　故原命题正确  ∴等腰三角形的底角必定是锐角.

　　说明：本例中“是锐角(小于90°)”的反面有“是直角(等于90°)”和“是钝角（大于90°)”两种情况，这时，必须分别证明命题结论反面的每一种情况都不可能成立，最后才能肯定命题的结论一定正确.此题是对反证法的进一步理解.

返回页首