第四节 圆心角、弧、弦、弦心距之间的关系

典型例题

　　例1、如图，已知：在⊙O中， =2 ，试判断∠AOB与∠COD，AB与2CD之间的关系，并说明理由.

　　分析：根据条件确定图形，观察、分析、猜想，特别是两条线段的不等关系，常常把两条线段放到一个三角形中.

　　解：∠AOB=2∠COD， AB<2CD，理由如下：

　如图，在⊙O上取一点C ’，使 = .∴∠COD=∠DOC’

　　　∵ =2 ，∴， = + = .

　　　∴AB=CC’. ∠AOB=∠CO C’=∠COD+∠DOC’=2∠COD

　　　又∵在△CDC’中，CD+DC’> CC’，∴CC’<2CD，即AB<2CD.

　　说明：此题进一步理解定理及其推论的应用条件，在“相等”问题中的不等量.由 =2 可得∠AOB=2∠COD是正确的，但由 =2 得出AB=2CD，是错误的，培养学生在学习中的迁移能力.

　　例2、如图，已知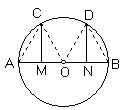：AB是⊙O直径，M、N分别是AO、BO的中点，CM⊥AB，DN⊥AB，求证： = .

　　分析：要证弧相等，可以证弧对应的弦相等，弧对应的圆心角相等.

　　证法一：连结AC、OC、OD、BD，

　　　∵M、N分别是AO、BO的中点，CM⊥AB，DN⊥AB，

　　　∴AC= OC、OD=BD

　　　又∵OC=OD，∴AC= BD，∴ = .

　　证法二：连结OC、OD，

　　　∵M、N分别是AO、BO的中点，∴OM=AO，ON= BO，

　　　∵OA=OB，∴OM=ON，

　　　∵CM⊥AB，DN⊥AB，∴OC=OD，

　　　∴Rt△COM≌Rt△DON，∴∠COA=∠DOB，∴ = .

　　证法三、如图，分别延长CM、DN交⊙O于E、F，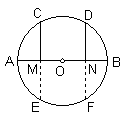

　　　∵M、N分别是AO、BO的中点，∴OM= AO，ON= BO，

　　　∵OA=OB，∴OM=ON，

　　　又∵CM⊥AB，DN⊥AB，∴CE=DF，∴ =

　　　∵ = ， = ，∴ = .

　　说明：此题是利用本节定理及推论应用的优秀题目，题目不难，但方法灵活，培养学生灵活解决问题的能力和基本的辅助线的作法.

　　例3、如图，已知：在⊙O中，OA⊥OB，∠A=35°，求 和 的度数.

　　分析：连结OC，通过求圆心角的度数求解.

　　解：连结OC，

　　　在Rt△AOB中，∠A=35°

　　　∴∠B=55°，又∵OC=OB，

　　　∴∠COB=180°-2∠B=70°，∴ 的度数为70°，

　　　∠COD=90°-∠COB=90°-70°=20°，

　　　∴ 的度数为20°.

　　说明：此题是基本题目，目的是巩固基础知识.

　　例4  如图，C是⊙O直径AB上一点，过C点作弦DE，使CD＝CO，若 的度数为40°，求 的度数．

　　分折： 要求 的度数，可求它所对的圆心角∠BOE的度数，如图作辅助线，通过等量转换得出结果．

　　解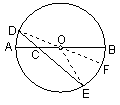： 连OE、OD并延长DO交⊙O于F．

　　　∵ 的度数为40°，∴∠AOD=40°．

　　　∵CD＝CO，  ∴∠ODE＝∠AOD＝40°．

　　　∵OD＝OE，  ∴∠E＝ ∠ODE＝40°．

　　　∴∠EOF=∠E+∠ODE=80°，∠BOF= ∠AOD＝40°，

　　　则∠BOE=∠EOF +∠BOF =80°+40°=120°，∴ 的度数为120°．

　　说明：此题充分体现了圆中的等量转换以及圆中角度的灵活变换．

返回页首