第二十节圆、扇形、弓形的面积　　　

作者：未知来源：中央电教馆时间：2006/4/8 18:03:14阅读：nyq

字号：小|大

典型例题

　　例1、如图，已知半径OA=6cm，C为OB的中点，∠AOB=120°，求阴影部分的面积．

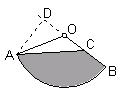　　解：过A作AD⊥BO交BO的延长线于D，

　　则AD是△ACO的边OC上的高，

　　∵∠AOB=120°，∴∠AOD=60°，

　　∴AD=OAsin60°= ．

　　∴S_阴影=S_扇形ABO-S_△ACO=

　　说明：（1）此题应用解直角三角形，三角形面积公式和扇形面积公式；（2）阴影部分的面积是由扇形和三角形组合而成，熟练拿握扇形面积公式和三角形面积公式是求此阴影部分面积的关键；（3）灵活选用三角形面积公式：

　　 ① ；② ．

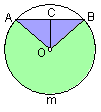
　　例2、已知：弓形的弧的度数为240°，弧长是，求弓形的面积．

　　解：如图，根据弧长公式有．

　　∴OA=2．∴ S_扇形OAmB= ，

　　S_△OAB= ，∴ ．

　　说明：（1）弓形面积的计算；（2）弓形面积可以看成是扇形面积和三角形面积的分解和组合，实际应用时，要注意公式的选择．

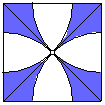
　　例3、如图，在边长l的正方形中，以各顶点为圆心，对角线长的一半为半径在正方形内画弧，则图中阴影部分的面积为_______．

　　解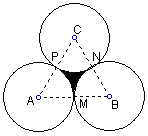：S_阴影= ．

　　说明：求面积问题的常用方法有：直接公式法，和差法，割补法等．

　　例4、如图，已知半径为1的三个等圆⊙A、⊙B、⊙C两两外切，切点分别为M、N、P，求夹在三个等圆中间的曲边形MNP的面积．

　　分析：连结AB、BC、CA，则必分别过点M、N、P．曲边形MNP如果先借添上三个全等扇形即构成了正△ABC，算出△ABC的面积后再还掉三个扇形．这样一借一还，先借后还，剩下的就是曲边形MNP．

　　解：S_曲边形MNP=

　　= ．

　　说明：求有关不规则图形的面积问题的关键是将图形分解为可求图形面积的和差问题，本题是作辅助线构造三角形和扇形的面积解决的．

备课资料