第五节 正弦、余弦的诱导公式

典型例题

　　例1  求 ．
　　分析：可用诱导公式一步化简求值．
　　解：原式


．
　　说明：准确记忆诱导公式是做此类题的关键．
　　例2  已知 ，求 的值．
　　分析：∵ ，因此可以把 化成 ，进而利用诱导公式求解．
　　解：∵ ，
　　　　∴ ，
　　　　故   原式 ．
　　说明：角变换是此题的关键，应注意掌握角变换的技巧．
　　例3  求证：
　　（1） ；
　　（2） ．
　　分析：∵ ，∴应对 进行奇、偶数两种情况的求解．
　　证明：   当 为奇数时，设 ，则
　　（1）
　　　　
　　　　 （此时 ）；
　　（2）
　　　　 ．
　　   当 为偶数时，设 ，则
　　（1）
　　　　 （此时 ）；
　　（2） ．
　　由 ， ，本题得证．
　　说明：要科学地应用诱导公式．
　　例4  已知 ，求证 ．
　　分析：由已知条件求出 与 的关系，再代入求证式化简．
　　解：∵ ，
　　∴ ， ，
　　
＝0．
　　说明：此题采用了由正弦、余弦诱导公式推得的正切的诱导公式，每一个读者都应掌握这种推导和应用公式的能力．
　　例5　化简：
　　（1） ；
　　（2） ， ．
　　分析：先用诱导公式将公子，分母分别化简，再约分化简．
　　解：（1）原式 ．
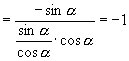　　（2）原式
　　　　　　　
　　　　　　　
　　　　　　　
　　　　　　　 ．
　　说明：由此题可见，“化弦”是最终化简的关键．

返回页首