 设为首页
设为首页
 加入收藏
加入收藏
例1.求 ![]() 的值.
的值.
分析:逆用二倍角公式,或构造对偶式列方程求解.
解:解法一:
![]()
![]()
![]() ,
,
∴ ![]() .
.
解法二:
原式 ![]()
![]() .
.
解法三:令 ![]() ,
, ![]() .
.
则 ![]()
![]()
![]() .
.
∵ ![]() ,∴
,∴ ![]() .
.
从而有 ![]() .
.
小结:对于本题,如若简单地从形式上看,为利用二倍角正弦公式而同乘同除式子
![]() ;或原式
;或原式 ![]() 后,简单地应用二倍角的余弦公式都将无益于问题的解决,反而会陷入思维的简单循环之中.因此,当我们面对一个较为陌生的问题时,应认真分析问题的特征,积极地进行联想化归,切实做到缜密稳妥地设计解题思路.
后,简单地应用二倍角的余弦公式都将无益于问题的解决,反而会陷入思维的简单循环之中.因此,当我们面对一个较为陌生的问题时,应认真分析问题的特征,积极地进行联想化归,切实做到缜密稳妥地设计解题思路.
(1)有些数学问题,可根据其本身特点,相应地构设与其相同“匹配”的另一整体,然后由其“相依而伴”的关系进行求解.如解法三,这种解题方法称为积式配对.
(2)角度成等比(公比为2)的同名弦函数的乘积通常可按解法一、二来求解.
例2.设 ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
分析:观察问题的角度状况,从已知条件和被求式的角度差异来看,一方面应将条件中的角度变换为
![]() 、
、 ![]() ,另一方面应将被求式中的角度
,另一方面应将被求式中的角度 ![]() 、
、 ![]() 变换为
变换为 ![]() 、
、 ![]() .要实现上述想法只需将两已知条件相乘,将被求式利用升幂公式即可办到.解:两已知条件相乘,可得
.要实现上述想法只需将两已知条件相乘,将被求式利用升幂公式即可办到.解:两已知条件相乘,可得
![]() ,
,
化简为 ![]() ,
,
∴ ![]()
![]() .
.
小结:根据问题的具体特点,从变换已知条件和被求式的角度入手,进行双向变换实现角度的统一,然后利用代入法将已知条件代入被求式,从而达到求值的目的,这就是解答本题的脉络.
例3.已知 ![]() ,
, ![]() .求
.求 ![]() 的值.
的值.
分析:若对结论“切化弦”后再化简不难发现,只需求出 ![]() 和
和 ![]() 的值即可,注意到
的值即可,注意到 ![]() ,就可以发现求解的途径了.
,就可以发现求解的途径了.
解:∵ ![]() ,∴
,∴ ![]() .
.
又∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
, ![]() .
.
又∵ ![]()
![]() ,
,
∴原式 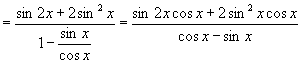
![]()
![]() .
.
小结:(1)本题也可以由 ![]() 得
得 ![]() ,再将要求解的三角式化为用
,再将要求解的三角式化为用 ![]() 表示的形式.
表示的形式.
(2)本题解法中巧妙地利用了“角的变换” ![]() ,使求解过程不致于繁杂.
,使求解过程不致于繁杂.
(3)若不注意 ![]() 的范围,就会导致由
的范围,就会导致由 ![]() 求出
求出 ![]() 而不知取舍.
而不知取舍.
例4.设 ![]() ,
, ![]() ,
, ![]() .求证:
.求证: ![]() .
.
分析:条件恒等式的证明,要注意观察条件和结论之间的差异.主要是看角,看函数的名称、次数.对于本题,从角的差异入手,将角变形为
![]() ,
, ![]() ,从已知条件变形入手,可证得结论.
,从已知条件变形入手,可证得结论.
证明:由 ![]() ,得
,得![]() ,
,
![]()
![]()
整理,得 ![]() .
.
为 ![]() ,
, ![]() ,将上式两边同除以
,将上式两边同除以![]() ,得
,得 ![]() .
.
小结:证明条件恒等式,一般有两种方法,即推出法与代入法,无论使用哪一种思路都要盯住目标,据果变形.若用推出法,则应盯住欲证等式的左、右两边,根据它们的状况(一般要看角、函数名称、次数),采取恰当的措施来对条件等式进行变形,直到目标.若用代入法,就要盯住作为目标的被证等式的一边,根据它对欲证等式的另一边及条件进行变形,先创造机会,然后代入条件,最终推出目标.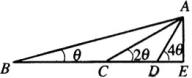
例5.如图,在某点 ![]() 处测得建筑物
处测得建筑物 ![]() 的顶端
的顶端 ![]() 的仰角为
的仰角为 ![]() ,沿
,沿 ![]() 方向前进30米至点
方向前进30米至点 ![]() 处测得顶端
处测得顶端 ![]() 的仰角为
的仰角为 ![]() ,再继续前进
,再继续前进 ![]() 米至
米至 ![]() 点,测得顶端仰角为
点,测得顶端仰角为 ![]() ,求
,求 ![]() 的大小和建筑物
的大小和建筑物 ![]() 的高.
的高.
分析:根据题意结合图形观察给出各数据间的关系,将题目数学化,抽象为纯数学问题.
解:由已知, ![]() 米,
米, ![]() 米
米
在 ![]() △
△ ![]() 中,
中, ![]() ,
,
在 ![]() △
△ ![]() 中,
中,![]()
∴ ![]() ,同理可得:
,同理可得:
![]()
于是: ![]() 即
即 ![]()
而 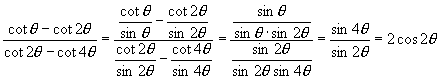
∴ ![]()
![]() ,
,
∴ ![]() 米
米
于是: ![]() ,建筑物高为15米.
,建筑物高为15米.
小结:这是一个三角函数在测量方面的应用问题,在解决过程中运用了几何知识和方程的思想,但三角式的化简起到了关键作用.