第五节 研究性课题与实习作业 线性规划的实际应用

　　例 某人有楼房一幢，室内面积共 ，拟分隔成两类房间作为旅游客房，大房间每间面积为 ，可住游客5名，每名游客每天住宿费为40元；小房间每间面积为 ，可住游客3名，每名游客每天住宿费为50元；装修大房间每间需1000元，装修小房间每间需600元，如果他只能筹款8000元用于装修，且游客能住满客房，他应隔出大房间和小房间各多少间，能获得最大利益？

　　分析：解线性规划问题，应该引入所需要的未知数，根据题设条件建构起约束条件和目标函数，再求最优解，但实际问题往往是“整数规划”，所以，如果所求最优解不是整点，那它就不是实际问题的解，因此，在最优解不是整点时，为求得问题的解，还应在可行域内在最优解“附近”去搜索使目标函数取得最大值的整点．

　　解：设隔出大房间 间，小房间 间，收益记为 元，则得线性约束条件

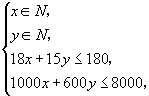                                   ①

　　同时，也有线性目标函数

            

　　这明显是一个整数规划问题，为求得 取最大的 ，我们可先减弱一下约束条件①

                                     ②

作出约束条件式③的可行域（如右图）

　　作直线 ．

　　把直线 向右上方平移至 位置时，直线经过可行域的点 ，并且与原点距离最大，此时 取得最大值．

　　解方程组

      

　　得     

　　由于点 的坐标不是整数，因而不是问题的解，为了得到问题的解，应在可行域内于点 附近搜索使 最大的点 ．

　　过点 作 ，容易识别可行域内位于 右上方无整点，而直线 上有两个整点： 和 ．故得问题的解是：

    或

并且 （元）．

　　答：应隔出小房间12间，或大房间3间、小房间8间，可以获得每天最大的收益为1800元．

返回页首