第七节 圆的方程

典型例题

　　例1：圆 上到直线 的距离为 的点共有（ ）．

　　（A）1个    （B）2个    （C）3个     （D）4个

　　分析：把 化为 ，圆心为 ，半径为 ，圆心到直线的距离为 ，所以在圆上共有三个点到直线的距离等于 ，所以选C．

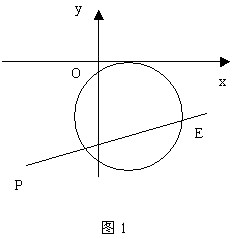　　例2：过点 作直线 ，当斜率为何值时，直线 与圆 有公共点，如图1所示．

　　解：设直线 的方程为

　　即

　　根据 有

　　整理得

　　解得

．

　　例3：求与 轴相切，圆心在直线 上，且被直线 截下的弦长为 的圆的方程．

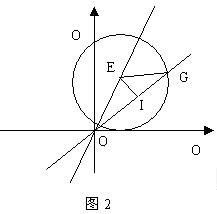　　解：设圆心坐标为 ，则半径 ，如图2

　　根据 有

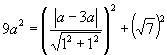
　　求得

　　则 的坐标为（1，3）或 ，半径为3．

　　所以，圆的方程为

或 ．

　　例4： 已知圆 ，求过点 与圆 相切的切线．

　　解：∵点 不在圆 上，

　　∴切线 的直线方程可设为

　　根据

　　∴                         

　　解得                       

　　所以                      

　　即                         

　　因为过圆外一点作圆得切线应该有两条，可见另一条直线的斜率不存在．易求另一条切线为 ．

　　说明：上述解题过程容易漏解斜率不存在的情况，要注意补回漏掉的解．

　　本题还有其他解法，例如把所设的切线方程代入圆方程，用判别式等于0解决（也要注意漏解）．还可以运用 ，求出切点坐标 、 的值来解决，此时没有漏解．

　　例5：自点 发出的光线 射到 轴上，被 轴反射，反射光线所在的直线与圆 相切

　　（1）求光线 和反射光线所在的直线方程．

　　（2）光线自 到切点所经过的路程．

　　分析、略解：根据对称关系，首先求出点 的对称点 的坐标为 ，其次设过 的圆 的切线方程为

根据 ，即求出圆 的切线的斜率为

或

　　进一步求出反射光线所在的直线的方程为

或

　　最后根据入射光与反射光关于 轴对称，求出入射光所在直线方程为

或

光路的距离为 ，可由勾股定理求得 ．

　　说明：本题亦可把圆对称到 轴下方，再求解．

　　例6：已知对于圆 上任意一点 ，不等式 恒成立，求实数 的取值范围．

　　解：运用圆的参数方程，设 的坐标为 ，

即 ， ，

　　∵ 恒成立

　　∴ 恒成立

　　即 恒成立

　　∴只需 大于等于 的最大值．

　　令

的最大值为

　　∴

　　说明：在上述解法中我们运用了圆上点的参数设法．采用这种设法的优点在于，一方面可以减少参数的个数，另一方面可以灵活地运用三角公式．从代数的观点看，这种设法的实质就是三角代换．

　　另外本题也可以不用圆的参数方程求解，本题的实质就是求最值问题，方法较多．但以上述解法较简．

返回页首