设为首页
加入收藏
当前位置:第一节 椭圆及其标准方程
作者：未知来源：中央电教馆时间：2006/4/8 18:03:15阅读：nyq
字号：小|大
典型例题（一）（例1～例5）
例1 已知椭圆
的一个焦点为（0，2）求 
的值．
分析：把椭圆的方程化为标准方程，由
，根据关系 
可求出 
的值．
解：方程变形为 
．
因为焦点在 
轴上，所以 
，解得 
．
又 
，所以 
， 
适合．故 
．
例2 已知椭圆的中心在原点，且经过点
， 
，求椭圆的标准方程．
分析：因椭圆的中心在原点，故其标准方程有两种情况．根据题设条件，运用待定系数法，求出参数
和 
（或 
和 
）的值，即可求得椭圆的标准方程．
解：当焦点在 
轴上时，设其方程为 
．
由椭圆过点 
，知 
．又 
，代入得 
， 
，故椭圆的方程为 
．
当焦点在 
轴上时，设其方程为 
．
由椭圆过点 
，知 
．又 
，联立解得 
， 
，故椭圆的方程为 
．
例3 
的底边 
， 
和 
两边上中线长之和为30，求此三角形重心 
的轨迹和顶点 
的轨迹．
分析：（1）由已知可得 
，再利用椭圆定义求解．（2）由 
的轨迹方程 
、 
坐标的关系，利用代入法求 
的轨迹方程．
解： （1）以 
所在的直线为 
轴， 
中点为原点建立直角坐标系．设 
点坐标为 
，由 
，知 
点的轨迹是以 
、 
为焦点的椭圆，且除去轴上两点．因 
， 
，有 
，故其方程为 
．
（2）设 
， 
，则 
．
①
由题意有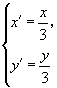 
代入①，得 
的轨迹方程为 
，其轨迹是椭圆（除去 
轴上两点）．
例4 已知 
点在以坐标轴为对称轴的椭圆上，点 
到两焦点的距离分别为 
和 
，过 
点作焦点所在轴的垂线，它恰好过椭圆的一个焦点，求椭圆方程．
分析：讨论椭圆方程的类型，根据题设求出
和 
（或 
和 
）的值．从而求得椭圆方程．
解：设两焦点为 
、 
，且 
， 
．
从椭圆定义知 
．即 
．
从 
知 
垂直焦点所在的对称轴，
所以在 
中， 
，
可求出 
， 
，从而 
．
∴所求椭圆方程为 
或 
．
例5 已知椭圆方程
，长轴端点为 
， 
，焦点为 
， 
， 
是椭圆上一点， 
， 
．求： 
的面积（用 
、 
、 
表示）．
分析 求面积要结合余弦定理及定义求角
的两邻边，从而利用 
求面积．
解：如图，设 
，由椭圆的对称性，不妨设 
，
由椭圆的对称性，不妨设
在第一象限．由余弦定理知：
· 
．①
由椭圆定义知：
②
则 
得
．
故 
．
典型例题（例6～例9）
例6
已知椭圆 
，
（1）求过点
且被 
平分的弦所在直线的方程；
（2）求斜率为2的平行弦的中点轨迹方程；
（3）过
引椭圆的割线，求截得的弦的中点的轨迹方程；
（4）椭圆上有两点
、 
， 
为原点，且有直线 
、 
斜率满足 
，求线段 
中点 
的轨迹方程．
分析 此题中四问都跟弦中点有关，因此可考虑设弦端坐标的方法．
解：设弦两端点分别为
， 
，线段 
的中点 
，则
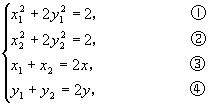
①－②得
．
由题意知
，则上式两端同除以 
，有 
，
将③④代入得
．
⑤
（1）将
， 
代入⑤，得 
，故所求直线方程为
．
⑥
将⑥代入椭圆方程
得 
， 
符合题意，故 
即为所求．
（2）将
代入⑤得所求轨迹方程为：
．（椭圆内部分）
（3）将
代入⑤得所求轨迹方程为
．（椭圆内部分）
（4）由①＋②得
，
⑦
将③④平方并整理得
，
⑧
，
⑨
将⑧⑨代入⑦得
，
⑩
再将
代入⑩式得
，
即
．
此即为所求轨迹方程．当然，此题除了设弦端坐标的方法，还可用其它方法解决．
例7
已知动圆 
过定点 
，并且在定圆 
的内部与其相内切，求动圆圆心 
的轨迹方程．
分析 关键是根据题意，列出点P满足的关系式．
解：如图所示，设动圆
和定圆 
内切于点 
．动点 
到两定点，即定点 
和定圆圆心 
距离之和恰好等于定圆半径，即 
．
∴点
的轨迹是以 
， 
为两焦点，半长轴为4，半短轴长为 
的椭圆的方程： 
．
说明：本题是先根据椭圆的定义，判定轨迹是椭圆，然后根据椭圆的标准方程，求轨迹的方程．这是求轨迹方程的一种重要思想方法．
例8
已知椭圆 
及直线 
．
（1）当
为何值时，直线与椭圆有公共点？
（2）若直线被椭圆截得的弦长为
，求直线的方程．
分析
直线与椭圆有公共点，等价于它们的方程组成的方程组有解．因此，只须考虑方程组消元后所得的一元二次方程的根的判别式．已知弦长，由弦长公式就可求出
．
解：（1）把直线方程
代入椭圆方程 
得
，即 
．
，
解得
．
（2）设直线与椭圆的两个交点的横坐标为
， 
，由（1）得
， 
．
根据弦长公式得
．
解得
．
因此，所求直线的方程为
．
说明
处理有关直线与椭圆的位置关系问题及有关弦长问题，采用的方法与处理直线和圆的有所区别．这里解决直线与椭圆的交点问题，一般考虑判别式
；解决弦长问题，一般应用弦长公式．用弦长公式，若能合理运用韦达定理（即根与系数的关系），可大大简化运算过程．
例9
以椭圆 
的焦点为焦点，过直线 
上一点 
作椭圆，要使所作椭圆的长轴最短，点 
应在何处？并求出此时的椭圆方程．
分析
椭圆的焦点容易求出，按照椭圆的定义，本题实际上就是要在已知直线上找一点，使该点到直线同侧的两已知点（即两焦点）的距离之和最小，而这种类型的问题在初中就已经介绍过，只须利用对称的知识就可解决．
解：如图所示，椭圆
的焦点为 
， 
．
点
关于直线 
的对称点 
的坐标为（－9，6），直线 
的方程为 
．解方程组 
得交点 
的坐标为（－5，4）．此时 
最小．
所求椭圆的长轴
，
∴
，又 
，
∴
．
因此，所求椭圆的方程为
．
说明 解决本题的关键是利用椭圆的定义，将问题转化为在已知直线上求一点，使该点到直线同侧两已知点的距离之和最小．