第四节 双曲线的几何性质

典型例题（例1～例4）

　　例1　求与双曲线 共渐近线且过 点的双曲线方程及离心率．

　　解法一：双曲线 的渐近线方程为：

　　（1）设所求双曲线方程为

　　∵ ，∴                    ①

　　∵ 在双曲线上

　　∴                           ②

　　由①－②，得方程组无解

　　（2）设双曲线方程为

　　∵ ，∴                              ③

　　∵ 在双曲线上，∴            ④

　　由③④得 ，

　　∴所求双曲线方程为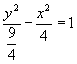： 且离心率

　　解法二：设与双曲线 共渐近线的双曲线方程为：

　　∵点 在双曲线上，∴

　　∴所求双曲线方程为： ，即 ．

　　评述：（1）很显然，解法二优于解法一．

　　（2）不难证明与双曲线 共渐近线的双曲线方程 ．

　　一般地，在已知渐近线方程或与已知双曲线有相同渐近线的条件下，利用双曲线系方程 求双曲线方程较为方便．通常是根据题设中的另一条件确定参数 ．

　　（3）以上优美巧妙的解法，达到了化繁为易的目的．教学中，要引起重视．

　　例2 作方程 的图象．

　　分析：∵ ，∴ ，∴

　　∴方程图象如右图，

　　即表示双曲线 的右支．

　　例3 作方程 的图象．

　　分析：∵

　　∴方程图象应该是圆 及双曲线 在 轴上方的图象．（画图请自行完成．）

　　评述：在根据方程作出相应图象时，应遵循：“如果曲线 的方程是 ，那么点 在曲线 上的充要条件是 ”这一原则；另外，须注意方程变形的未知数的允许值可能会扩大，而原方程的曲线只能取原方程允许值范围内的那一部分．

　　例4 求以曲线 和 的交点与原点的连线为渐近线，且实轴长为12的双曲线的标准方程．

　　分析：先求出渐近线方程，确定出其斜率，结合已知条件确定所求双曲线方程中的字母系数．

　　解：∵ ，∴ 或 ，

　　∴渐近线方程为

　　当焦点在 轴上时，由 且 ，得 ．

　　∴所求双曲线方程为

　　当焦点在 轴上时，由 ，且 ，得 ．

　　∴所求双曲线方程为

　　评述：（1）“定量”与“定位”是求双曲线标准方程的两个过程，解题过程中应准确把握．

　　（2）为避免上述的“定位”讨论，我们可以用有相同渐近线的双曲线系方程去解，请读者自行完成．

典型例题（例5～例10）

　　例5 已知双曲线的渐近线方程为 ，两条准线间的距离为 ，求双曲线标准方程．

　　分析：可根据双曲线方程与渐近线方程的关系，设出双曲线方程，进而求出双曲线标准方程．

　　解：∵双曲线渐近线方程为 ，∴设双曲线方程为

　　（1）若 ，则 ，

　　∴准线方程为： ，∴ ，∴

　　（2）若 ，则 ，

　　∴准线方程为： ，

　　∴ ，

　　∴

　　∴所求双曲线方程为： 或

　　评述：（1）准确及进地应用有相同渐近线的双曲线系方程给我们的求解过程带来了方便．

　　（2）通过待定系数法求出参数 ．

　　例6 中心在原点，一个焦点为 的双曲线，其实轴长与虚轴长之比为 ，求双曲线标准方程．

　　解：设双曲线的标准方程为 ，则 ，

　　解得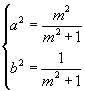

　　∴ 为所求双曲线的标准方程．

　　评述：以上方法是求双曲线标准方程的通用方法，注意其中的运算技巧．

　　例7　求中心在原点，对称轴为坐标轴经过点 且离心率为 的双曲线标准方程．

　　解：设所求双曲线方程为： ，则 ，

　　∴ ，∴ ，∴所求双曲线方程为

　　评述：（1）以上巧妙简捷的设法是建立在一个事实的基础上的，即离心率 是双曲线的等轴双曲线的充要条件，它的证明如下：

　　设等轴双曲线 ，则 ，

　　∴

　　∴ ，∴

　　反之，如果一个双曲线的离心率 ．

　　∴ ，∴ ， ，∴ ，

　　∴ ，

　　∴双曲线是等轴双曲线

　　（2）还可以证明等轴双曲线的其他性质：两条渐近线互相垂直；等轴双曲线上任意一点到中心的距离是它到两个焦点的距离的比例中项等．

　　例8　已知点 ， ，在双曲线 上求一点 ，使 的值最小．

　　解：∵ ， ，∴ ，∴

　　设点 到与焦点 相应准线的距离为 则

　　∴ ，∴

　　至此，将问题转化成在双曲线上求一点 ，使 到定点 的距离与到准线距离和最小．即到定点 的距离与准线距离和最小为直线 垂直于准线时，解之得，点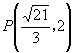

　　评述：灵活巧妙地运用双曲线的比值定义于解题中，将会带给我们意想不到的方便和简单．教学中应着重培养学生灵活运用知识的能力．

　　例9 已知： 是双曲线 上一点．

　　求：点 到双曲线两焦点 、 的距离．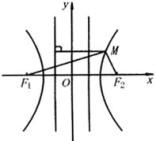

　　分析：利用双曲线的第二定义．

　　解：如图，设点 到相应焦点 、 的准线的距离为 、 ．

　　当 点在双曲线的右支上时， ，且有

　　∴ ，



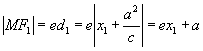　　当点 在双曲线的左支上时， ，且有

　　∴ ，



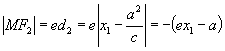
　　评述：以上结论称为双曲线的焦点半径公式，它在解题过程中发挥着很大的优越性，可使解题过程的运算量简化，从而得到避繁就简效果．例如：

　　在双曲线 的一支上有三个不同点 、 、 与焦点 的距离成等差数列，求 的值．

　　解：直接利用焦半径公式，得： ， ，

　　∴ ，

　　∴ ，即

　　注意：一般地，在涉及到双曲线上的点到焦点的距离问题，应用焦半径公式是一种简单快捷的方法．

　　例10 如图所示，已知梯形 中， ，点 满足 ，双曲线过 、 、 三点，且以 、 为焦点，当 时，求双曲线离心率的取值范围．

　　分析一：依题意，建立恰当的坐标系，并通过 、 、 的坐标及双曲线的方程求解．

　　解法一：以直线 为 轴，以 的垂直平分线为 轴，建立直角坐标系 ，则 轴，因双曲线过点 、 ，且以 、 为焦点，由双曲线的对称性可知 、 关于 轴对称．

　　设 、 、 ，其中 为双曲线的半焦距， 是梯形的高．

　　由 ，即 ，

得 ，

　　设双曲线方程为 ，则离心率为 ．

　　由点 、 在双曲线上，将 、 的坐标和 ，代入双曲线方程得



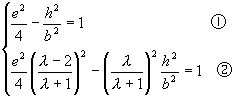
　　由①得 ，将③代入②式中，整理得：

　　∴ ，又∵ ，∴ ，

　　∴

　　∴双曲线的离心率取值范围为 ．

　　分析二：建立直线 方程，再与双曲线方程联立，借助一元二次方程根与系数关系解题．

　　解法二：前面部分同解法一．

　　可求得直线 方程为 ，将其代入双曲线方程 中，得

　　又∵ 、 为上述二次方程的两根，∴ ①

　　又∵ 在双曲线上，∴ ②

　　∵ 　　　　　　　　　　　③

　　将②③代入①中，得：

　　∵ ，∴

　　以下同解法一

　　分析三：借助焦半径公式解题．

　　∵ ，∴ 　　　　　　　　　　　　①

　　∴ ，由焦半径公式，得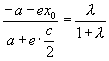： 　　　②

　　将①代入②，得：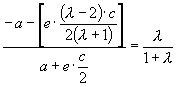

　　∵ ，∴

　　以下同解法一

　　评述：（1）此题的关键是：弄清应设定几个量之间关系（如： 、 、 、 ）．难点：如何自始至终保持思路清晰，有条不紊．

　　（2）比较以上三种方法不难发现：解法二虽思路简单自然，但由于采取了联立方程消元的思想，也就导致了解题过程的运算繁琐，这对于学生的计算能力要求是很高的，解法三因巧妙地运用了焦半径公式，使得求解过程变得简洁快捷，而且给人以一种心满意足的感觉，这表明善于记忆一些中间结果对我们的学习帮助很大．