 设为首页
设为首页
 加入收藏
加入收藏
例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个?
分析与解:分析个位数字,可分以下几类.
个位是9,则十位可以是1,2,3…,8中的一个,故有8个;
个位是8,则十位可以是1,2,3…,7中的一个,故有7个;
与上同样:
个位是7的有6个;
个位是6的有5个;
……
个位是2的只有1个.
由分类计数原理知,满足条件的两位数有
![]() (个).
(个).
说明:本题是用分类计数原理解答的,结合本题可加深对“做一件事,完成之可以有n类办法”的理解,所谓“做一件事,完成它可以有n类办法”,这里是指对完成这件事情的所有办法的一个分类.分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次分类时要注意满足一个基本要求:完成这件事的任何一种方法必须属于某一类,并且分别属于不同两类的两种方法是不同的方法,只有满足这些条件,才可以用分类计数原理.
 例2
在由电键组A与B所组成的并联电路中,如图,要接通电源,使电灯发光的方法有多少种?
例2
在由电键组A与B所组成的并联电路中,如图,要接通电源,使电灯发光的方法有多少种?
解:因为只要合上图中的任一电键,电灯即发光,由于在电键组A中有2个电键,电键组B中有3个电键,应用分类计数原理,所以共有:
2+3=5种接通电源使灯发亮的方法。
例3 二年级一班有学生56人,其中男生38人,从中选取一名男生和一名女生作代表,参加学校组织的调查团,问选取代表的方法有几种.
分析与解:男生38人,女生18人,
由分步计数原理共有![]() (种)
(种)
答:选取代表的方法有684种.
说明:本题是用分步计数原理解答的,结合本题可以加深对“做一件事,完成之需要分成n个步骤”的理解,所谓“做一件事,完成它需要分成n个步骤”,分析时,首先要根据问题的特点,确定一个分步的可行标准;其次,分步时还要注意满足完成这件事情必须并且只需连续完成这对![]() 个步骤后,这件事情才算圆满完成,这时,才能使用来法原理.
个步骤后,这件事情才算圆满完成,这时,才能使用来法原理.
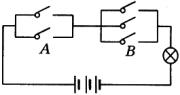 例4 在电键组A、B组成的串联电路中,如图,要接通电源使灯发光的方法有几种?
例4 在电键组A、B组成的串联电路中,如图,要接通电源使灯发光的方法有几种?
解:只要在合上A组中两个电键之后,再合上B组中3个电键中的任意一个,才能使电灯的电源接通,电灯才能发光,根据分步计数原理共有:
2×3=6种不同的方法接通电源,使电灯发光。
例5 有10本不同的数学书,9本不同的语文书,8本不同的英语书,从中任取两本不同类的书,有多少种不同取法?
分析:任取两本不同类的书,有三类:一、取数学、语文各一本;二、取语文、英语各一本;三、取数学、英语各一本.然后求出每类取法,利用分类计数原理即可得解.
解:取出两本书中,一本数学一本语文有![]() 种不同取法,一本语文一本英语有
种不同取法,一本语文一本英语有![]() 种不同取法,一本数学,一本英语有
种不同取法,一本数学,一本英语有![]() 种不同取法.
种不同取法.
由分类计数原理知:共有![]() 种不同取法.
种不同取法.
说明:本例是一个综合应用分步计数原理和分类计数原理的题目,在处理这类问题时,一定要搞清哪里是分类,哪里是分步,以确定利用加法或分步计数原理.
例6(1993年全国高考题)同室4人各写1张贺年卡,先集中起来,然后每人从中各拿1张别人送出的贺年卡,则4张贺年卡不同的分配方式有( )
A.6种 B.9种 C.11种 D.23种
分析:本题完成的具体事情是四个人,每人抽取一张贺卡,问题是按照一定要求,抽取结果有多少种不同情况.我们可以把抽卡片的过程分成四步,先是第一人抽,然后第二人,以此类推,但存在的问题是,我们把四个人记为![]() 、
、![]() 、
、![]() 、
、![]() ,他们的卡片依次记为
,他们的卡片依次记为![]() 、
、![]() 、
、![]() 、
、![]() ,如果第一步
,如果第一步![]() 抽取
抽取![]() ,接着
,接着![]() 可抽
可抽![]() 、
、![]() 、
、![]() ,有三种方法,而
,有三种方法,而![]() 抽
抽![]() 或
或![]() ,
,![]() 仅有两种抽法,这样两步之间产生影响,这样必须就
仅有两种抽法,这样两步之间产生影响,这样必须就![]() 抽的结果进行分类.
抽的结果进行分类.
解法1:设四人A,B,C,D写的贺年卡分别是a,b,c,d,当A拿贺年卡b,则B可拿a,c,d中的任何一个,即B拿a,C拿d,D拿c或B拿c,D拿a,C拿d或B拿d,C拿a,D拿c,所以A拿b时有三种不同分配方法.同理,A拿c ,d时也各有三种不同的分配方式.由分类计数原理,四张贺年卡共有3+3+3=9种分配方式.
解法2:让四人A,B,C,D依次拿一张别人送出的贺年卡.如果A先拿有3种,此时写被A拿走的那张贺年卡的人也有3种不同的取法.接下来,剩下的两个人都各只有一种取法.由分步计数原理,四张贺年卡不同的分配方式有![]() 种.
种.
∴ 应选B.
注意:(1)本题从不同的角度去思考,从而得到不同的解答方法,解法1是用分类计数原理解答的,解法2是用分步计数原理解答的.在此有必要再进一步对两个原理加以理解:
如果完成一件事的各种方法是相互独立的,那么计算完成这件事的方法数时,使用分类计数原理.
如果完成一件事的各个步骤是相互联系的,即各个步骤都必须完成,这件事才告完成,那么计算完成这件事的方法数时,使用分步计数原理.
(2)分类计数原理、来法原理是推导排列数、组合数公式的理论基础,也是求解排列、组合问题的基本思想方法,这两个原理十分重要必须认真学好,并正确地灵活加以应用.
(3)如果把四个人依次抽取的结果用一个图表体现出来,就显得更加清楚.

共有9种不同结果.
这个图表我们称之为“树形图”,在解决此类问题往往很有效,通过它可以把各种不同结果直观地表现出来.
例1 计算:(1)![]() ;
(2)
;
(2)![]() .
.
分析:本题如果直接计算组合数,运算比较繁.本题应努力在式子中创造条件使用组合数的性质,第(1)题中,![]() ,经此变形后,可继续使用组合数性质.第(2)题有两个考虑途径,一方面可以抓住项的变形
,经此变形后,可继续使用组合数性质.第(2)题有两个考虑途径,一方面可以抓住项的变形![]() ,求和;另一方面,变形
,求和;另一方面,变形![]() ,接着
,接着![]() ,
,![]() …,反复使用公式.
…,反复使用公式.
解:(1)原式![]()
![]() .
.
(2)原式![]()
![]() .
.
另一方法是:原式![]()
![]()
![]() .
.
说明:利用第(2)小题的手段,我们可以得到组合数的一个常用的结论:
![]() .
.
左边![]() 右边.
右边.
例2 从7名男生5名女生中,选出5人,分别求符合下列条件的选法种数有多少种?
(1)![]() 、
、![]() 必须当选;(2)
必须当选;(2)![]() 、
、![]() 都不当选;(3)
都不当选;(3)![]() 、
、![]() 不全当选;(4)至少有2名女生当选;(5)选出5名同学,让他们分别担任体育委员、文娱委员等5种不同工作,但体育委员由男生担任,文娱委员由女生担任.
不全当选;(4)至少有2名女生当选;(5)选出5名同学,让他们分别担任体育委员、文娱委员等5种不同工作,但体育委员由男生担任,文娱委员由女生担任.
分析:本题是组合应用题中典型的选代表问题,通过一些明确的条件对结果进行限制.问题(1)![]() 、
、![]() 必须当选,它们就不必再考虑,只要再选出余下的代表.问题(2)
必须当选,它们就不必再考虑,只要再选出余下的代表.问题(2)![]() 、
、![]() 必须不当选,实际上就是去掉这几个元素不予考虑.问题(3)
必须不当选,实际上就是去掉这几个元素不予考虑.问题(3)![]() 、
、![]() 不全当选可以从正反两方面考虑.从正面考虑可以按
不全当选可以从正反两方面考虑.从正面考虑可以按![]() 、
、![]() 全不选和
全不选和![]() 、
、![]() 选一个分类,从反面考虑可用间接法,去掉
选一个分类,从反面考虑可用间接法,去掉![]() 、
、![]() 全选的情况.问题(4)可以按女生选2人、3人…进行分类,当然也可以从反面考虑用间接法.问题(5)可以先处理特殊位置的体育班委与文娱班委.
全选的情况.问题(4)可以按女生选2人、3人…进行分类,当然也可以从反面考虑用间接法.问题(5)可以先处理特殊位置的体育班委与文娱班委.
解:(1)除![]() 、
、![]() 选出外,从其它10个人中再选3人,共有的选法种数为
选出外,从其它10个人中再选3人,共有的选法种数为![]()
![]() (种).
(种).
(2)去掉![]() 、
、![]() ,从其它10人中任选5人,共有的选法种数为:
,从其它10人中任选5人,共有的选法种数为:![]() (种).
(种).
(3)按![]() 、
、![]() 的选取情况进行分类:
的选取情况进行分类:![]() 、
、![]() 全不选的方法数为
全不选的方法数为![]() ,
,![]() 、
、![]() 选1人的方法数为
选1人的方法数为![]() ,共有选法
,共有选法![]() (种).
(种).
本小题的另一解法:从12人中选5人的选法中去掉![]() 、
、![]() 全选的情况,所有选法只有
全选的情况,所有选法只有![]() (种).
(种).
方法一:按女同学的选取情况分类:
选2名女同学、3名男同学;选3名女同学2名男同学;选4名女同学1名男同学;选5名女同学.所有选法数为:
![]() (种).
(种).
方法二:从反面考虑,用间接方法,去掉女同学不选或选1人的情况,所有方法总数为:![]() (种).
(种).
(5)选出一个男生担任体育班委,再选出1名女生担任文娱班委,剩下的10人中任取3人担任其它3个班委.用分步计数原理可得到所有方法总数为:![]() (种).
(种).
说明:对于本题第(4)小题,“至少有2名女生当选”,我们可能还有另外一种考虑,先从5名女生中选出2人,然后在剩下的10人中任选3人,得到的方法数为![]() (种),与上述答案比较,结果明显增多了,为什么会出现以上情况?上述步骤得到的选取结果虽然符合了有2名女生的要求,但在计数时出现了重复,比如先选两女生为
(种),与上述答案比较,结果明显增多了,为什么会出现以上情况?上述步骤得到的选取结果虽然符合了有2名女生的要求,但在计数时出现了重复,比如先选两女生为![]() 、
、![]() ,剩下的10人中如果又选出了女生
,剩下的10人中如果又选出了女生![]() ,与先选两名女生为
,与先选两名女生为![]() 、
、![]() 后又选出了女生
后又选出了女生![]() ,出现了同样的结果,因为选取问题仅考虑选出了哪些元素,至于先选后选并不考虑.这里需要我们引起注意的是以后遇到“至少”类型的问题,一般采用分类法或间接法解决,在选取问题中尽可能避免出现重复计数,我们还可以进一步从下一个例子加深理解.
,出现了同样的结果,因为选取问题仅考虑选出了哪些元素,至于先选后选并不考虑.这里需要我们引起注意的是以后遇到“至少”类型的问题,一般采用分类法或间接法解决,在选取问题中尽可能避免出现重复计数,我们还可以进一步从下一个例子加深理解.
例3 空间10个点,其中有5点在同一个平面内,其余无三点共线,四点共面,问以这些点为顶点,共可构成多少个四面体?
分析:本题如果从正面考虑可以按5个共面的点的选用情况进行分类.如果从反面考虑用间接法,只要去掉从5个共面的点中任取四个点的情况,因为共面的四个点不能构成四面体的四个顶点.
解:方法一:可以按共面的点取0个、1个、2个、3个进行分类,得到所有的取法总数为:![]() 个.
个.
方法二:从10个点中任取4个点的方法数中去掉4个点全部取自共面的5个点的情况,得到所有构成四面体的方法数为:![]() (个).
(个).
说明:以几何为背景的此类应用题中,间接方法用得比较多,在考虑去掉不符合要求的选法时,既不能多去,也不能少去,此外有时还需去掉一些重复计数的情况.比如:四面体的顶点和各条棱的中点共10个点,任取其中的4个点,其中不共面的取法有多少种?我们可以从10个点中任取4点.共有![]() 种取法,然后去掉下面几种情况,4个点取在四面体的同一个面上,有
种取法,然后去掉下面几种情况,4个点取在四面体的同一个面上,有![]() 种取法;四个中点连成平行四边形的情形,有3种取法,还有3点在四面体的一条棱上,另一点是其它点,不考虑已计算的四点在四面体同一面上的情况,共有6种取法.用间接法可得不同的取法共有:
种取法;四个中点连成平行四边形的情形,有3种取法,还有3点在四面体的一条棱上,另一点是其它点,不考虑已计算的四点在四面体同一面上的情况,共有6种取法.用间接法可得不同的取法共有:![]() (种).
(种).
例4 在1,3,5,7,9中任取3个数字,在0,2,4,6,8中任取两个数字,可组成多少个不同的五位偶数.
分析:因为零不能作首位数,所以是特殊元素,因此可以根据选零不选零为分类标准。
解:第一类:五位数中不含数字零。
第一步:选出5个数字,共有![]() 种选法.
种选法.
第二步:排成偶数—先排末位数,有![]() 种排法,再排其它四位数字,有
种排法,再排其它四位数字,有![]() 种排法.
种排法.
∴ ![]() (个)
(个)
第二类:五位数中含有数字零.
第一步:选出5个数字,共有![]() 种选法。
种选法。
第二步:排顺序又可分为两小类;
(1)末位排零,有![]() 种排列方法;
种排列方法;
(2)末位不排零.这时本位数有![]() 种选法,而因为零不能排在首位,所以首位有
种选法,而因为零不能排在首位,所以首位有![]() 种排法,其余3个数字则有
种排法,其余3个数字则有![]() 种排法.
种排法.
∴ ![]()
∴ 符合条件的偶数个数为
![]()
![]() (个)
(个)
说明:本题也可以用间接法(即排除法)来解.请读者自行完成.
例5 有12名划船运动员,其中3人只会划左舷,4人只会划右舷,其余5人既会划左舷也会划右舷。现在要从这12名运动员中选出6人平均分在左、右舷划船参加比赛,有多少种不同的选法?
分析:设集合A={只会划左舷的3个人},B={只会划右舷的4个人},C={既会划左舷又会划右舷的5个人}
先分类,以集合A为基准,划左舷的3个人中,有以下几类情况:①A中有3人;②A中有2人;C中有1人;③A中有1人,C中有2人;④C中有3人。
第①类,划左舷的人已选定,划右舷的人可以在![]() 中选3人,即有
中选3人,即有![]() 种选法。因是分步问题,所以有
种选法。因是分步问题,所以有![]() 种选法。第②类,划左舷的人在A中选2人,有
种选法。第②类,划左舷的人在A中选2人,有![]() 种选法,在C中选1人,有
种选法,在C中选1人,有![]() 种选法,划右舷的在
种选法,划右舷的在![]() 中剩下的8个人中选3人,有
中剩下的8个人中选3人,有![]() 种选法。因是分步问题,所以有
种选法。因是分步问题,所以有![]() 种选法。类似地,第③类,有
种选法。类似地,第③类,有![]() 种选法。第④类有
种选法。第④类有![]() 种选法。
种选法。
因为是分类,所以一共有![]() 种选法。
种选法。
解:![]()
![]()
![]() 种
种
答:一共有2174种不同选法.
说明:这种比较复杂的在若干个集合中选取元素的问题,只要能运用分类思想正确对所求选法分类,又能正确地根据题目要求合理地考察步骤,就可以顺利地求得解.在分类时,要注意做到既不重复也不遗漏.
这里是以集合A为基准进行分类,也可以集合B或集合C为基准进行分类,其结果是相同的,但一般都选择元素个数较少的集合作为基准来分类,这样可以减少分类,方便运算.
例6 甲、乙两队各出7名队员,按事先排好的顺序出场参加围棋擂台赛,双方由1号队员出赛,负者被淘汰,胜者再与负方2号队员比赛,…,直到一方队员全被淘汰为止,另一方获胜,形成一种比赛过程,试求所有可能出现的比赛过程的种类.
分析与解:若甲队取胜,比赛结果可能是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 只有一个过程;
只有一个过程;
![]() 共8场,乙队在前7场中胜一场,有
共8场,乙队在前7场中胜一场,有![]() 种不同的过程;
种不同的过程;
![]() 共9场,乙队在前8场中胜二场,有
共9场,乙队在前8场中胜二场,有![]() 种不同的过程;
种不同的过程;
![]() 共10场,乙队在前9场中胜三场,有
共10场,乙队在前9场中胜三场,有![]() 种不同的过程;
种不同的过程;
………………
∴ 甲队取胜的过程种数是:![]()
类似乙队取胜也有同样的过程种数
∴ 共有![]() 种不同的比赛过程.
种不同的比赛过程.
小结:一个排列与另一个排列的区别有两点,一点是元素不同,另一点是顺序不同(在元素相同时);而一个组合与另一个组合不同点仅是元素不同,由此可知,排列是有顺序问题,组合是无顺序问题.本题是一应用问题,根据实际确定是组合问题.
例7 从1到9的九个数字中取三个偶数四个奇数,试问:
(1)能组成多少个没有重复数字的七位数?
(2)上述七位数中三个偶数排在一起的有几个?
(3)(1)中的七位数中,偶数排在一起、奇数也排在一起的有几个?
(4)(1)中任意两偶然都不相邻的七位数有几个?
分析与解:(l)分步完成:第一步在4个偶数中取3个,可有![]() 种情况;第二步在5个奇数中取4个,可有
种情况;第二步在5个奇数中取4个,可有![]() 种情况;第三步3个偶数,4个奇数进行排列,可有
种情况;第三步3个偶数,4个奇数进行排列,可有![]() 种情况,所以符合题意的七位数有
种情况,所以符合题意的七位数有![]() 个.
个.
(2)上述七位数中,三个偶数排在一起的有![]() 个.
个.
(3)上述七位数中,3个偶数排在一起,4个奇数也排在一起的有
![]() 个.
个.
(4)上述七位数中,偶数都不相邻,可先把4个奇数排好,再将3个偶数分别插入5个空档,共有![]() 个.
个.
说明;对于有限制条件的排列问题,常可分步进行,先组合再排列,这是乘法原理的典型应用.
例8 6本不同的书,按照以下要求处理,各有几种分法?
(1)一堆一本,一堆两本,一堆三本;
(2)甲得一本,乙得两本,丙得三本;
(3)一人得一本,一人得二本,一人得三本;
(4)平均分给甲、乙、丙三人;
(5)平均分成三堆.
分析与解:(1)先在6本书中任取一本.作为一本一堆,有![]() 种取法,再从余下的五本书中任取两本,作为两本一堆,有
种取法,再从余下的五本书中任取两本,作为两本一堆,有![]() 种取法,再后从余下三本取三本作为一堆,有
种取法,再后从余下三本取三本作为一堆,有![]() 种取法,故共有分法
种取法,故共有分法![]() 种.
种.
(2)由(1)知.分成三堆的方法有![]() 种,而每种分组方法仅对应一种分配方法,故甲得一本,乙得二本,丙得三本的分法亦为
种,而每种分组方法仅对应一种分配方法,故甲得一本,乙得二本,丙得三本的分法亦为![]() 种.
种.
(3)由(1)知,分成三堆的方法有![]() 种,但每一种分组方法又有
种,但每一种分组方法又有![]() 不同的分配方案,故一人得一本,一人得两本,一人得三本的分法有
不同的分配方案,故一人得一本,一人得两本,一人得三本的分法有![]() (种).
(种).
(4)3个人一个一个地来取书,甲从6本不同的书本中任取出2本的方法有![]() 种,甲不论用哪一种方法取得2本书后,已再从余下的4本书中取书有
种,甲不论用哪一种方法取得2本书后,已再从余下的4本书中取书有![]() 种方法,而甲、乙不论用哪一种方法各取2本书后,丙从余下的两本中取两本书,有
种方法,而甲、乙不论用哪一种方法各取2本书后,丙从余下的两本中取两本书,有![]() 种方法,所以一共有
种方法,所以一共有![]() 种方法.
种方法.
(5)把6本不同的书分成三堆,每推二本与把六本不同的书分给甲、乙、丙三人,每人二本的区别在于,后者相当于把六本不同的书,平均分成三难后,再把每次分得的三堆书分给甲、乙、丙三个人.因此,设把六本不同的书,平均分成三堆的方法有![]() 种,那么把六本不同的书分给甲、乙、丙三人每人2本的分法就应
种,那么把六本不同的书分给甲、乙、丙三人每人2本的分法就应![]() 种,由(4)知,把六本不同的书分给甲、乙、丙三人,每人2本的方法有
种,由(4)知,把六本不同的书分给甲、乙、丙三人,每人2本的方法有![]() 种.
种.
所以![]() ,则
,则![]() (种)
(种)
说明:本问题中的每一个小题都提出了一种类型问题,搞清类型的归属对今后解题大有补益,其中
(1)属非均匀分组问题. (2)属非均匀定向分配问题.
(3)属非均匀不定向分配问题.(4)属均匀不定向分配问题.
(5)属均匀分组问题.
例9 有6本不同的书,分给甲、乙、丙三个人.
(1)如果每人得两本,有多少种不同的分法;
(2)如果一个人得一本,一个人得2本,一个人得3本有多少种不同的分法;
(3)如果把这6本书分成三堆,每堆两本有多少种不同分法.
分析与解:(1)假设甲先拿,则甲从6本不同的书中选取2本有![]() 种方法,不论甲取走的是哪两本书,乙再去取书时只能有
种方法,不论甲取走的是哪两本书,乙再去取书时只能有![]() 种,此时剩下的两本书自然给丙,就只有
种,此时剩下的两本书自然给丙,就只有![]() 种方法,由乘法原理得一共有
种方法,由乘法原理得一共有![]() 种不同分法.
种不同分法.
(2)先假设甲得1本,乙得2本,丙得3本则有![]() 种法,一共有
种法,一共有![]() 种不同的分法.
种不同的分法.
(3)把6本书分成三堆,每堆2本,与次序无关.
所以一共有![]() 种不同分法.
种不同分法.
说明:本题的三个问题要注意区别和联系,不要混淆.
6本书分给甲、乙、丙三人每人两本和分成3堆每堆两本是有区别的,前者虽然也属均分问题,但要甲、乙、丙三个人一个人一个人的去拿,而后者属均分问题又是无序问题,所以必须除以![]() .一般地,
.一般地,![]() 个元素中有
个元素中有![]() 个元素(
个元素(![]() )均分成m堆一定要除以
)均分成m堆一定要除以![]() .
.
例如:有17个桃,分成8堆,其中一堆一个,一堆4个,另外6堆每堆都是2个,有多少种不同的分法.
一共有![]() 种不同分法.
种不同分法.