第三节 复数的向量表示

例1 用复数表示下图中各题的阴影部分．

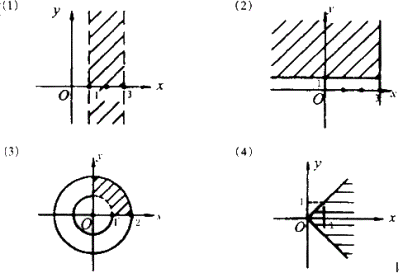
　　解：设复数 ，则：

　　（1）

　　（2） 且

　　（3） ，且 且

　　（4） ，且

例2 设 ，在复平面上画出满足下列条件的点Z的集合所表示的图形：（1） 且 ；

　　（2） ，且 ；

　　（3） 且 ．

　　解 （1）∵ 且 ，∴表示虚轴右边的阴影部分（不含虚轴），又∵ ，故不含原点，如右图．

　　（2）∵ ，且 表示由 ， 四条直线围成的矩形，如右图中阴影部分，包括周界AD，BC，但不包括周界AB，CD及矩形内部的实轴部分．

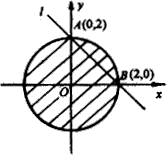　　（3）因为满足 的图形足以（0，0）为原心，2为半径的圆及其内部．满足 的图形是直线 ．同时满足上述两条件的图形是直线 被圆O截得的弦，即以A（0，2），B（2，0）为端点的弦AB，如右图所示．

例3已知复数 ， ，且 ，求实数 的取值范围．

　　分析：题中 和 都是虚数，而虚数与虚数，虚数与实数之间不能比较大小，但 ， 都是实数，它们之间是可以比较大小的，可利用复数模的定义来列出关于 的不等式．

　　解：由已知 ，

　　∵ ， ∴ ，解之

例4 设 ， ， ．若全集 ， ，那么 中所有 在复平面上对应的点的集合是什么图形？

　　分析：解决复数在复平面上对应的几何图形问题，要熟练掌握两点：①复数 在复平面上对应点Z（ ）；② 的几何含意为 在复平面上对应点Z与原点的距离．本题关键是求出 的取值范围，就可确定 在复平面上的图形．

　　解：由已知： ；

        

　　∴ ，

　　∴    

　　∴ 在复平面上对应的点Z的集合应是与原点距离大于1而不大于3的所有点．

　　∴ 中的所有 在复平面上对应的点的集合是以原点为圆心，以1和3为半径的圆所夹的圆环，但不包括小圆的边界（如右图）．

例5 已知 ，求复数Z．

　　分析1：设 转化为实数问题

　　解：设 ，依题意得



　　即

　　根据复数相等条件是



　　解得：

 ∴

　　分析2：从已知条件中直接求出 ，进而求出 ．

　　解：由已知可得 ，等式两边取模得 ．两边平方得 ．把 代入原方程可得 ．

　　说明：本例的解法1是通过复数相等条件把复数问题转化为实数来解决的．而解法2则是直接利用复数 的性质来求解的．这两种解法是解决复数问题的两种基本方法．