 设为首页
设为首页
 加入收藏
加入收藏
典型例题(一)
例1 计算
(1) ![]() ; (2)
; (2) ![]() ;
;
(3) ![]()
分析:根据复数加、减法运算法则进行运算。
解:(1) ![]()
(2) ![]()
(3) ![]()
![]()
![]()
例2 设复数满足 ![]() ,求
,求 ![]() 的最大值和最小值。
的最大值和最小值。
分析:仔细地观察、分析等式 ![]() ,实质是一实数等式,由其特点,根据实数的性质知若
,实质是一实数等式,由其特点,根据实数的性质知若 ![]() ,则
,则 ![]() ,因此已知等式可化为
,因此已知等式可化为 ![]()
解:由已知等式得 ![]()
 即
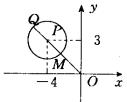
即 ![]() ,它表示的以点P(-4,3)为圆心,半径
,它表示的以点P(-4,3)为圆心,半径 ![]() 的圆面。
的圆面。
如图可知 ![]() 时,
时, ![]() 有最大值
有最大值 ![]() ;
; ![]() 时
时 ![]() 有最小值
有最小值 ![]()
小结:求复数的模的最值常常根据其几何意义,利用图形直观来解。
例3
复数 ![]() ,
, ![]() ,
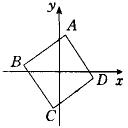
, ![]() ,它们在复平面上的对应点是一个正方形的三个顶点,求这个正方形的第四个顶点对应的复数。
,它们在复平面上的对应点是一个正方形的三个顶点,求这个正方形的第四个顶点对应的复数。
分析1:利用 ![]() 或者
或者 ![]() 求点D对应的复数。
求点D对应的复数。
解法1:设复数 ![]() ,
, ![]() ,
, ![]() 所对应的点分别为A、B、C,正方形的第四个顶点D对应的复数为
所对应的点分别为A、B、C,正方形的第四个顶点D对应的复数为 ![]() (
( ![]() )则
)则![]()
![]()
![]()
![]()
![]()
∵
![]()
∴ ![]()
∴
![]() 解得
解得 ![]()
故点D对应的复数 ![]()
分析2:利用正方形的性质,对角钱相等且互相平分,相对顶点连线段的中点重合,即利用正方形的两条对角线交点是其对称中心求解.
解法2:设复数 ![]() ,
, ![]() ,
, ![]() 所对应的点分别为A、B、C,正方形的第四个顶点D对应的复数为
所对应的点分别为A、B、C,正方形的第四个顶点D对应的复数为 ![]() (
( ![]() )
)
因为点A与点C关于原点对称,所以原点O为正方形的中心.
∴
点O也是B与D点的中点,于是由
![]()
∴
![]()
故D对应的复数为 ![]()
小结:解题1一定要善于发现问题中可能被利用的条件,寻找最佳的解题方法,解法2利用正方形是如C对称固形,解题思路较巧.
典型例题(二)
例4
已知 ![]() ,
, ![]() (
(![]() )分别对应向量
)分别对应向量 ![]() ,
, ![]() (O为原点),若向量
(O为原点),若向量 ![]() 对应的复数为纯虚数,求
对应的复数为纯虚数,求
![]() 的值。
的值。
分析: ![]() 对应的复数为纯虚数,利用复数减法先求出
对应的复数为纯虚数,利用复数减法先求出
![]() 对应的复数,再利用复数为纯虚数的条件求解即得。
对应的复数,再利用复数为纯虚数的条件求解即得。
解:设向量 ![]() 对应复数
对应复数 ![]()
∵ ![]()
∴ ![]()
![]()
![]()
∵
![]() 为纯虚数,∴
为纯虚数,∴
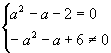 即
即 ![]()
∴ ![]()
例5
![]() ,求
,求 ![]() 对应的点的轨迹方程.
对应的点的轨迹方程.
解: ![]() ,则
,则 ![]()
又 ![]() ,故有
,故有 ![]()
∴
![]()
∴
![]() 对应点的轨迹是以
对应点的轨迹是以 ![]() 为圆心,
为圆心, ![]() 为半径的圆.
为半径的圆.
小结:由减法的几何意义知 ![]() 表示复平面上两点
表示复平面上两点 ![]() ,
, ![]() 间的距离.
间的距离.
当 ![]() ,表示复数
,表示复数 ![]() 对应的点的轨迹是以
对应的点的轨迹是以 ![]() 对应的点为圆心,半径为
对应的点为圆心,半径为 ![]() 的圆.
的圆.
当 ![]()
![]() ,表示以复数
,表示以复数 ![]() ,
, ![]() 的对应点为端点的线段的垂直平分线.
的对应点为端点的线段的垂直平分线.
当 ![]() (
( ![]() ),则表示以复数
),则表示以复数 ![]() ,
, ![]() 的对应点为焦点的椭圆.
的对应点为焦点的椭圆.
当 ![]() (
( ![]() ),则表示以复数
),则表示以复数 ![]() ,
, ![]() 的对应点为焦点的双曲线.
的对应点为焦点的双曲线.
例6
已知 ![]() (
( ![]() )且有
)且有 ![]() ,求满足上述条件的复数
,求满足上述条件的复数 ![]() 所对应的曲线,并将其画出.
所对应的曲线,并将其画出.
分析:不妨将复数 ![]() 写成代数式
写成代数式 ![]() ,由模的性质可将复数方程转化为代数方程,再确定它所表示的曲线.
,由模的性质可将复数方程转化为代数方程,再确定它所表示的曲线.
解:设 ![]() (
( ![]() 且不能同时为零)
且不能同时为零)
∵
![]()
∴
![]() ∴
∴ ![]() 或
或 ![]()
又
![]() ,
,
 ∵
∵ ![]()
故满足已知条件的复数Z所对应的曲线是圆 ![]() 及
及 ![]() 轴(不包括原点)在圆
轴(不包括原点)在圆 ![]() 的外部的那部分曲线,如图中粗线所示.
的外部的那部分曲线,如图中粗线所示.
例7
在复平面内, ![]() 的顶点O为坐标原点,顶点A、C对应的复数分别为
的顶点O为坐标原点,顶点A、C对应的复数分别为
![]() ,
, ![]() ,若点B在单位圆内,求实数
,若点B在单位圆内,求实数 ![]() 的取值范围。
的取值范围。
分析:要求点B在单位圆内,实际上是 ![]() ,只要求出点B对应的复数,利用模的定义就可求解。
,只要求出点B对应的复数,利用模的定义就可求解。
解:设点B对应的复数为 ![]()
根据平行四边形法则, ![]()
∴
![]()
由题意知 ![]()
![]() 即
即 ![]()
∴
![]()