 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
应用机械能守恒定律解题的一般步骤是:
1、明确研究对象,是由哪些物林组成的系统; 并正确分析系统内每个物体的受力情况。
2、判明各力做功情况。判断是否符合机械能守的适用条件。
3、该取零势能面,找出系统各物体初,末态的动能和势能。
4、应用机械能守恒定律列出表达式,解题过程中注意统一单位制。
扩展资料
机械能守恒定律解题的一般方法
1.选取合适的研究对象,对研究对象进行受力做功分析,判断研究对象机械能是否守恒。
2.选取某一物理过程进行研究,对选定的参考平面及参照系确定这一过程初末状态动能与势能。
3.根据机械能守恒定律列式求解,机械能守恒定律的表达式有三种:
①![]() ,②
,②![]() ,③
,③![]() 。
。
可根据题意,选择合适的表达式。
例 如图所示,总长为l的光滑均匀铁链,跨过一个光滑的轻质小滑轮,开始时底端相干,当略有扰动时其一端下沉,则铁链刚脱离滑轮的瞬间其速度为多大?
解答 以整条铁链为研究对象,因为铁链光滑,不受摩擦阻力,只受到重力和支持力。但支持力不做功,只有重力做功,所以铁链在运动过程中机械能守恒。
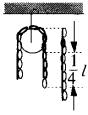 铁链的重心位置下降
铁链的重心位置下降![]() ,
,
如图中所示,所以,![]()
则根据机械能守恒定律:![]() ,即
,即![]() ,
,
![]()
点评: 利用机械能守恒定律的![]() 形式时,可以不选择参考平面,但必须正确确定初末状态下重心的位置。
形式时,可以不选择参考平面,但必须正确确定初末状态下重心的位置。
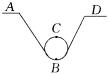 例 如图所示,大型露天游乐场中翻滚过山车质量为1t,从轨道一侧的顶端A处释放,到达底部B后又冲上环形轨道,使乘客头朝下地通过C点,再沿环形轨道到底部,最后冲上轨道另一侧的顶端D。如果不考虑车与轨道间的摩擦和空气阻力,已知轨道的最高点A比最低点B高20m,圆环半径为5m,试求:
例 如图所示,大型露天游乐场中翻滚过山车质量为1t,从轨道一侧的顶端A处释放,到达底部B后又冲上环形轨道,使乘客头朝下地通过C点,再沿环形轨道到底部,最后冲上轨道另一侧的顶端D。如果不考虑车与轨道间的摩擦和空气阻力,已知轨道的最高点A比最低点B高20m,圆环半径为5m,试求:
(1)过山车通过B点时的动能是多大?
(2)过山车通过C点的速度多大?
(3)过山车在D点的机械能多大?
解:
(1)过山车在整个运动过程不受摩擦阻力和空气阻力,机械能守恒。
过山车从A运动到B:
![]() 。
。
(2)过山车从A运动到C:

(3)![]()
点评 : 运用机械能守恒定律解题时,应灵活选取过程进行列式。
扩展资料
机械能守恒定律和动量守恒定律的区别
机械能守恒定律和动量守恒定律虽然研究对象都是相互作用的物体系,且研究的都是某一物理过程,但它们研究物理过程的出发点不同,因此处理问题的方法也完全不同,其主要区别为:
A.守恒的条件不同.
系统机械能是否守恒,决定于是否有重力(弹力)以外的力做功;系统动量是否守恒,决定于是否有外力作用.
B.受力分析出发点不同.
在利用机械能守恒定律处理问题时,要着重分析力做功情况,看看是否有重力(弹力)以外的力做功;在利用动量守恒定律处理问题时,着重分析系统受力情况(不管是否做功),并着重分析是否有外力作用.
C.列方程时注意点不同.
列机械能守恒定律方程首先要确定系统零势能位置,其定律表示成为标量式,任何情况下都不能分解和合成;列动量守恒定律方程前先要确定矢量的正方向,其定律表示成为矢量式,且可在某一方向应用.
D.必须注意,由于两个守恒定律的成立条件不同,所以系统机械能守恒时,动量不一定守恒.同样动量守恒的系统,机械能不一定守恒.
扩展资料
潮汐发电
由于引潮力的作用,使海水不断地涨潮、落潮.涨潮时,大量海水汹涌而来,具有很大的动能;同时,水位逐渐升高,动能转化为势能.落潮时,海水奔腾而去,水位陆续下降,势能又转化为动能.海水在运动中所具有的动能和势能统称为潮汐能.
潮汐能的重要应用之一是发电.潮汐发电就是在海湾或有潮汐的河口建筑一座拦水堤坝,形成水库,并在坝中或坝旁放置水轮发电机组,利用潮汐涨落时海水水位的升降,使海水通过水轮机时推动水轮发电机组发电.从能量的角度说,就是利用海水的势能和动能,通过水轮发电机转化为电能.潮汐发电的优点是成本低,每度电的成本只相当火电站的八分之一.
1913年德国在北海海岸建立了世界上第一座潮汐发电站.我国大陆海岸线长,潮汐能资源很丰富.1957年我国在山东建成了第一座潮汐发电站.据不完全统计,我国潮汐能蕴藏量为1.l亿千瓦,年发电量可达2750千瓦时,其中可供开发的约3850万千瓦,年发电量万870亿千瓦时,大约相当于40多个新安江水电站.