 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
电场线的知识结构
1、电场线是描述电场强度分布的一族曲线.描述方法:用曲线的疏密描述电场的强弱,用曲线某点的切线方向表示该点场强方向.
2、电场的特点:
(1)在静电场中,电场线从正电荷起,终于负电荷,不闭合曲线.
(2)电场线不能相交,否则一点将有两个场强方向.
(3)电场线不是电场里实际存在的线,是为使电场形象化的假想线.
3、点电荷的电场线.
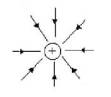
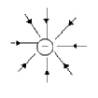
图中所示为正、负点电荷电场线的分布,应熟练掌握.
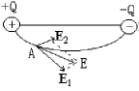
从上图可以看出,E1为+Q在A处的场强,E2为-Q在A处的场强,E为E1与E2的合场强,正好为电场线在A的切线。两个点电荷形成的电场中,每条电场线上每个点符合上述的关系。
4、匀强电场
(1)定义:在电场的某一区域里,如果各点场强大小和方向都相同,这个区域的电场就叫做匀强电场.
(2)电场线如下图所示.电场线互相平行的直线,线间距离相等.

(3)两块靠近、正对且等大的平行金属板,分别带等量正负电荷时,它们之间的电场是匀强电场.边缘附近除外.
扩展资料
电场线的有关内容简述
为了形象地表示出电场中各点场强的大小和方向,引入了电场线的图示法.
具体的作法是在电场中作出一系列的曲线,使曲线上每一点的切线方向都与该点的场强方向一致,这些曲线叫电场线.
要认识几种常见电场的电场线,包括正点电荷电场、负点电荷电场、两个等量异种点电荷电场、两个等量同种点电荷电场和匀强电场的电场线.其中的匀强电场是区域内各点场强大小和方向都相同的电场.
电场线的特点是:
(1)不闭合:从正电荷出发终止于负电荷;
(2)不中断:在无电荷的区域内不会中断;
(3)不相交:任意两条电场线不能相交.
电场线的作用:
(1)电场线上某一点的切线方向就是该点的场强方向,也是放在该点的正检验电荷所受电场力的方向;
(2)电场线的疏密程度表示场强的大小,电场线密的地方场强大,电场线疏的地方场强小.
扩展资料
电场线的应用
1、关于感应电荷问题
①感应电荷的绝对值小于或等于施感电荷的绝对值.如图所示,A是带正电的导体,电量为q,当它靠近中性导体B时,在B的近端产生感应负电荷-
![]() ,远端产生感应正电荷+
,远端产生感应正电荷+ ![]() .这里,若简单认为感应电荷量等于施感电荷量,即
.这里,若简单认为感应电荷量等于施感电荷量,即 ![]() ,则结论是错误的,事实上可以证明
,则结论是错误的,事实上可以证明
![]() .
.

导体在静电平衡下是个等势体,根据电场线性质,B的远端+ ![]() 发出的电场线不能终止于近端的-
发出的电场线不能终止于近端的- ![]() 上,只能终止于无穷远处,因此必有
上,只能终止于无穷远处,因此必有 ![]() .同理,从无穷远处来的电场线亦不能终止于导体B近端的-
.同理,从无穷远处来的电场线亦不能终止于导体B近端的- ![]() 上,因此,可以断定终止于B近端负电荷的电场线全部来自于A上的施感电荷.由高斯定理的几何意义,起始于A上施感正电荷的电场线条数为
上,因此,可以断定终止于B近端负电荷的电场线全部来自于A上的施感电荷.由高斯定理的几何意义,起始于A上施感正电荷的电场线条数为 ![]() ,终止于B近端上感应负电荷的电场线条数为
,终止于B近端上感应负电荷的电场线条数为 ![]() ..若注意到施感电荷+q发出的电场线可以部分终止于无穷远处或全部终止于B近端感应电荷-
..若注意到施感电荷+q发出的电场线可以部分终止于无穷远处或全部终止于B近端感应电荷- ![]() 上的事实,则有
上的事实,则有 ![]() .
.
在特殊情况下,施感电荷发出的电场线可以全部终止于感应电荷上,因而有 ![]() .譬如导体空腔内的施感电荷在腔内表面感应的电荷就属于这种情况.
.譬如导体空腔内的施感电荷在腔内表面感应的电荷就属于这种情况.
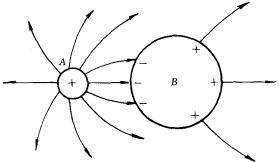
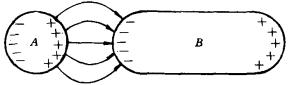 ②两个导体中(不论电荷量如何)至少有一个导体其表面上各点的面电荷密度不会异号.这一结论可采用反证法来证明.设A、B两个导体上都出现异号电荷,如图所示.又设
②两个导体中(不论电荷量如何)至少有一个导体其表面上各点的面电荷密度不会异号.这一结论可采用反证法来证明.设A、B两个导体上都出现异号电荷,如图所示.又设 ![]() ,则根据电场线性质,起始于A上正电荷的电场线必定有一部分终止于B上的负电荷,而终止于A上负电荷的电场线不可能起始于A上的电荷,因为A是一个等势体,当然也不可能起始于B上的正电荷,否则将导致
,则根据电场线性质,起始于A上正电荷的电场线必定有一部分终止于B上的负电荷,而终止于A上负电荷的电场线不可能起始于A上的电荷,因为A是一个等势体,当然也不可能起始于B上的正电荷,否则将导致
![]() 与题设相矛盾.因此,只可能起始于无穷远处,于是有
与题设相矛盾.因此,只可能起始于无穷远处,于是有 ![]() .同理可知,起始于B上正电荷的电场线既不能终止于B上的负电荷,也不能终止于A上的负电荷,只能终止于无穷远处.于是又
.同理可知,起始于B上正电荷的电场线既不能终止于B上的负电荷,也不能终止于A上的负电荷,只能终止于无穷远处.于是又 ![]() ,这与
,这与 ![]() 相矛盾.由此证明,原先假设A、B两导体同时带异号电荷是不可能的,可能的是两个导体中至少要有一个不同时带异号电荷.
相矛盾.由此证明,原先假设A、B两导体同时带异号电荷是不可能的,可能的是两个导体中至少要有一个不同时带异号电荷.
③带等量同号电荷的两相同导体球面不可能感应异号电荷.为确定起见,假定两导体球面上原来带的都是正电荷(负电荷可同样论证),且其中有一个球面上出现负感应电荷,则根据电场线性质应有电场线终止于该负电荷处.因为两导体球面的电势相等,所以终止于负电荷的电场线既不可能起始于同一球面,也不可能起始于另一球面,而只能起始于无穷远处.但是,球面上原有正电荷发出电场线是终止于无穷远处的,即无穷远处的电势比球面的电势要低,所以不可能有电场线是起始于无穷远而终止于导体球面的,这就证明了球表面不可能感应出负电荷.
2、关于电势问题
①在无电荷存在的真空静电场中,电势不可能有极值.设所论空间某点P的电势有极大值,则P点电势高于周围临近各点的电势.根据电场线性质3,必有电场线从P点发出,于是根据电场线性质,P点肯定有正电荷存在,这就与无电荷真空相矛盾,故P点电势不可能有极大值.同理可证P点电势也不可能有极小值.
②若所有导体电势都相等,则导体以外的无电荷空间中各点的电势均与各导体的电势相等.
设所论空间有三个导体,且 ![]() ,根据电场线性质,三个导体间彼此不可能有电场线相连接,空间可能有的电场线要么从三个导体发出终止于无穷远,要么从无穷远射来终止于这些导体上.若空间某点P电势与导体电势不相等,如
,根据电场线性质,三个导体间彼此不可能有电场线相连接,空间可能有的电场线要么从三个导体发出终止于无穷远,要么从无穷远射来终止于这些导体上.若空间某点P电势与导体电势不相等,如 ![]() ,则根据电场线性质3,过P点必有电场线指向导体,于是空间中必有电势为极大值的点,因为电势在没有电荷的空间是连续分布的,且空间的边界一个是U(三个导体),另一个是无穷远(
,则根据电场线性质3,过P点必有电场线指向导体,于是空间中必有电势为极大值的点,因为电势在没有电荷的空间是连续分布的,且空间的边界一个是U(三个导体),另一个是无穷远( ![]() ).显然,这种情况与前一结论相矛盾.同理可证
).显然,这种情况与前一结论相矛盾.同理可证 ![]() 将产生相同的矛盾.由于P点是任意取的,则命题得证.
将产生相同的矛盾.由于P点是任意取的,则命题得证.
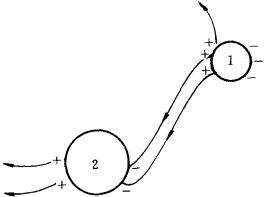 ③在除了导体以外没有其他电荷分布的情况下,若所有导体都是电中性的,则各导体的电势都相等,且为零.如图所示,设导体1与导体2电势不相等,如
③在除了导体以外没有其他电荷分布的情况下,若所有导体都是电中性的,则各导体的电势都相等,且为零.如图所示,设导体1与导体2电势不相等,如
![]() ,两个导体都是电中性,则根据电场线性质1、3,由导体1上正电荷发出的电场线,一部分将终止于导体2上的负电荷,另一部分将延伸到无穷远处;导体2上正电荷发出的电场线只能延伸到无穷远处;导体1上的负电荷是要终止电场线的,但这电场线既不能由导体1发出(导体是等势体),也不能接受导体2上发出的电场线(因
,两个导体都是电中性,则根据电场线性质1、3,由导体1上正电荷发出的电场线,一部分将终止于导体2上的负电荷,另一部分将延伸到无穷远处;导体2上正电荷发出的电场线只能延伸到无穷远处;导体1上的负电荷是要终止电场线的,但这电场线既不能由导体1发出(导体是等势体),也不能接受导体2上发出的电场线(因 ![]() ),更不能接受来自无穷远处的电场线,因为导体2已有电场线延伸到无穷远处,这就与假设
),更不能接受来自无穷远处的电场线,因为导体2已有电场线延伸到无穷远处,这就与假设 ![]() 相矛盾.采用同样的方法,不难证明对于
相矛盾.采用同样的方法,不难证明对于 ![]() 的所有情况都会出现类似的矛盾.因此,导体1和导体2的电势只能相等且为零,故结论得证.
的所有情况都会出现类似的矛盾.因此,导体1和导体2的电势只能相等且为零,故结论得证.
④中性孤立导体的电势等于零,表面电荷面密度处处为零.这个结论可用反证法加以论证.不妨假设孤立中性导体的电势U>0,则根据电场线性质,此导体表面某处必有电场线发出而终止于无穷远处,因此该处表面必有电荷存在.导体既然是电中性的,那么,由电荷守恒定律可以谁知,导体表面另外某处必有等量负电荷存在,同样由电场线性质可知负电荷上必有电场线终止,这些电场线唯一可能的来源只能是起始于无穷远处,因此有 ![]() ,显然,这和开始的假设相矛盾.若假设U<0,同样导致矛盾的结果.由此证明,中性孤立导体的电势只能等于零,其表面各点不可能有面电荷密度.
,显然,这和开始的假设相矛盾.若假设U<0,同样导致矛盾的结果.由此证明,中性孤立导体的电势只能等于零,其表面各点不可能有面电荷密度.
⑤中性导体B接近带负电的导体时,前者电势降低,后者电势升高.在中性导体B末进入带负电的导体A所激发的电场前,导体B属中性孤立导体,故由上述所证结论知,
![]() .当B接近导体A后,由于静电感应,其左右两端分别
.当B接近导体A后,由于静电感应,其左右两端分别  出现感应电荷,如图所示.根据电场线性质,终止于导体B右端负电荷的电场线只能起始于无穷远处,沿着这些电场线电场强度的积分
出现感应电荷,如图所示.根据电场线性质,终止于导体B右端负电荷的电场线只能起始于无穷远处,沿着这些电场线电场强度的积分
![]() ,因此,
,因此, ![]() ,而且B越接近A,右端感应的负电荷面密度越大,终止的电场线越密,由电场线性质知附近的电场强度也越大,因而
,而且B越接近A,右端感应的负电荷面密度越大,终止的电场线越密,由电场线性质知附近的电场强度也越大,因而 ![]() 越小(从无穷远处为电势参考点去考虑).与此同时,由于静电感应,A上负电荷向右端聚集,左端负电荷面密度减小,因而终止的电场线相应减少,A的左半空间的电场强度也减小,于是A的电势升高.同理可证,中性导体接近带正电的导体时,前者电势升,后者电势降低.
越小(从无穷远处为电势参考点去考虑).与此同时,由于静电感应,A上负电荷向右端聚集,左端负电荷面密度减小,因而终止的电场线相应减少,A的左半空间的电场强度也减小,于是A的电势升高.同理可证,中性导体接近带正电的导体时,前者电势升,后者电势降低.
3、关于导体接地问题
 ①接地导体的电势等于零,地球与无穷远同电势,即
①接地导体的电势等于零,地球与无穷远同电势,即
![]() .
.
先讨论如图所示的情形,如果B是一个很大的导体球,则B的远端离A的距离就很大,远端表面也很大.因此,远端的感应电荷面密度
![]() 与A表面电荷面密度及B近端表面电荷面密度比较就显得很小,故远端附近的电场线也就很疏.根据电场线性质可知远端表面附近的电场强度与A附近的电场强度比较也很小,沿着这些电场线电场强度E的线积分
与A表面电荷面密度及B近端表面电荷面密度比较就显得很小,故远端附近的电场线也就很疏.根据电场线性质可知远端表面附近的电场强度与A附近的电场强度比较也很小,沿着这些电场线电场强度E的线积分 ![]() 也很小,即
也很小,即 ![]() 很小.设想当B的半径
很小.设想当B的半径 ![]() ,则远端电荷面密度
,则远端电荷面密度 ![]() ,远端表面附近的电场强度
,远端表面附近的电场强度 ![]() ,因而
,因而 ![]() .
.
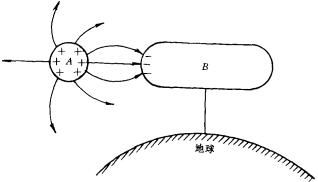
再讨论导体B接地时的情形(如图),这时B和地球组成一个导体,地球的另一侧成了这个导体的远端,因为地球半径很大,所以 ![]() .
.
在以上的讨论中,我们认为地球是一个很大的导体球,且是电中性的,并将无穷远区取在地球之外,得出 ![]() .实际上,所讨论的带电体的线度与地球半径相比往往是非常小的,而离带电体足够远处就可视为无穷远,所以实际上无穷远处仍在地球上.带电体在该处产生的电场已小得足以忽略.由于带电体在地球上感应的电荷面密度在离带电体足够远处也近乎于零,因此,地球是电中性的.这样,在无穷远区就没有电场,因此,无穷远处为等电势区域,且与地球的电势相等.这样,我们又得到了
.实际上,所讨论的带电体的线度与地球半径相比往往是非常小的,而离带电体足够远处就可视为无穷远,所以实际上无穷远处仍在地球上.带电体在该处产生的电场已小得足以忽略.由于带电体在地球上感应的电荷面密度在离带电体足够远处也近乎于零,因此,地球是电中性的.这样,在无穷远区就没有电场,因此,无穷远处为等电势区域,且与地球的电势相等.这样,我们又得到了 ![]() .但这与以前的不同,以前的无穷远区在地球之外,现在的无穷远区在地球之上了!事实上,我们讨论静电平衡问题都属于这种情况.
.但这与以前的不同,以前的无穷远区在地球之外,现在的无穷远区在地球之上了!事实上,我们讨论静电平衡问题都属于这种情况.
②孤立导体接地后,表面电荷面密度处处为零.设孤立导体接地后其表面某处有 ![]() ,则由电场线性质可知,该处必有电场线发出,又根据电场线性质,这些电场线不能终止于导体自身,只能终止于无穷远处,因此有
,则由电场线性质可知,该处必有电场线发出,又根据电场线性质,这些电场线不能终止于导体自身,只能终止于无穷远处,因此有 ![]() ,显然,这就与接地导体的电势等于零的结论相矛盾.如设导体表面处有
,显然,这就与接地导体的电势等于零的结论相矛盾.如设导体表面处有 ![]() ,同样导致矛盾结果.由此证明接地导体表面电荷面密度处处为零.
,同样导致矛盾结果.由此证明接地导体表面电荷面密度处处为零.
③接地导体附近若只有一个带电体,则接地导体表面不可能有与带电体上的电荷同号的电荷.
上述结论还与接地线在什么位置无关,.
4、关于孤立带电导体电场的能量问题
设孤立导体的电容为C,所带的电量为Q,则由普物静电场理论可知,孤立导体所激发的电场具有总能量
![]() .下面我们同样用电场线有关性质来证明这个结论.
.下面我们同样用电场线有关性质来证明这个结论.
如图所示,为确定起 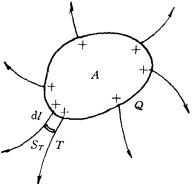 见,设孤立导体A所带电量
见,设孤立导体A所带电量 ![]() ,根据电场线性质,它发出的所有电场线都将延伸到无穷远处,其中T为一束细电场线管.已知静电场能量密度为
,根据电场线性质,它发出的所有电场线都将延伸到无穷远处,其中T为一束细电场线管.已知静电场能量密度为 ![]() ,现在对整个T管取
,现在对整个T管取 ![]() 的体积分,即:
的体积分,即:
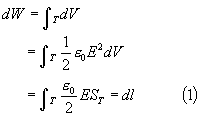
式中 ![]() 为T管上的任一横截面积,
为T管上的任一横截面积, ![]() 为沿T管方向的线元,
为沿T管方向的线元, ![]() 为整个T管中的电场能量.
为整个T管中的电场能量.
根据电场线性质,电场线管T内的电场线条数到处一样, ![]() 常数,于是,( l)式中的
常数,于是,( l)式中的 ![]() 因子可提出积分号,即:
因子可提出积分号,即:
![]() (2)
(2)
因为 ![]() 所以(2)式可改写为:
所以(2)式可改写为:
![]() (3)
(3)
若对孤立导体A发出的所有电场线管求和,则可求得孤立导体A所激发电场的总能量为:
![]() (4)
(4)
(4)式中为孤立导体A发出的电场线总条数.由高斯定理的几何意义知,孤立导体发出的电场线总条数为
![]() ,于是(4)可改写为:
,于是(4)可改写为:
![]() (5)
(5)
(5)式就是我们所要证明的结论.
扩展资料
电场线的主要性质
概括起来,电场线有如下一些性质:
(1)电场线起始于正电荷(或无穷远处),终止于负电荷(或无穷远处),它是一条连续曲线,决不会在没有电荷的地方中断.由E和电场线的定义可以得出这个结论.
(2)在没有点电荷的空间里,电场线不相交.因为根据库仑定律和电场强度的叠加原理,电荷在空间每一点产生的电场强度都是唯一的,因而静电场中每一点总场强E的方向都是唯一的,而E的方向就是电场线方向,所以电场线不可能相交.
(3)电场线的方向总是指向电势降落的方向.这个结论可由E沿电场线方向的积分得出.设a、b为电场线上的任意商点,则沿电场线积分便有:
![]() (1)
(1)
或者由场强与电势的负梯度关系:
![]() ▽U
(2)
▽U
(2)
可知,电场线方向是电势U在空间下降最陡的方向.电场线性质(3)与电场线上任意两点的电势都不能相等等价.
(4)电场线不形成闭合曲线.这个结论可由(1)式和静电场的环路定理:
![]() (3)
(3)
得出.因为假定电场线闭合,则由(1)式令b与a重合,沿这闭合的电场线积分一圈,便有
![]() ,而这与(3)式矛盾,故假定不合理,即电场线不能闭合.
,而这与(3)式矛盾,故假定不合理,即电场线不能闭合.
(5)电场线与等势面正交.
(6)电场线密度等于电场强度的大小,电场线密处表示电场强度大,电场线疏处表示电场强度小.
电场线上述诸性质不仅是描绘电场线图像的依据,而且也是定性、定量分析与讨论静电平衡问题的有用工具,只要与静电平衡条件下导体的性质配合得当.下面我们就用电场线性质来讨论若干问题,从中得出一些对中学物理教学有帮助的结论.