第八节 电容器 电容

电容器的串联和并联

一、串联把几个电容器一个接一个地联在一起．串联电容器的等效电容 、电压 、电量 与每个电容器的电容、电压、电量的关系为：

电容器串联后电容减小，每个电容器上的电压只是总电压的一部分．通常利用串联电容器来提高耐压．

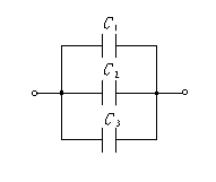
二、并联把几个电容器的一个极板联在一起，另一个级板也联在一起．并联电容器的等效电容 、电压 、电量 与每个电容器的电容、电压、电量的关系为：

通常利用电容器并联来增大电容．

关于电容器电容的定义问题

　　一般普通物理书中把电容器的电容定义为：两个任意形状、互相靠近的导体，在周围没有其他导体或带电体时，它们就组成了一个电容器，每一个导体就是该电容器的一个极板。如果两极板上分别带有等量异号的电荷＋Q与－Q，它们相应的电势分别为 与 ，实验表明，Q与 成正比，比值 叫做电容器的电容。

　　不少学生提出问题：如果两个极板上不是带等量异号电荷，而是分别带有电荷 与 ，此时电容器的电容能否仍用 定义？如果可以，那么式中的Q指的是什么电荷？对此问题的解答是，电容器的电容仍可用 定义，式中Q是指要使电容器两极板电势相等时，从一个极板向另一个极板转移的电量， 是电量Q转移之前两极板之间原有的电势差。

　　为了对上述结论作出证明，让我们先引进电容系数概念。

　　导体系的电容理论研究的是，在线性介质内导体系的电量与电势的关系。所谓线性介质是指电位移矢量D与场强E成线性关系，在这里表现为导体系的电量与电势成线性关系。设有N个导体组成的导体系，除大地外不受其他外部导体的影响，如N等于2时，导体系就是一个电容器。

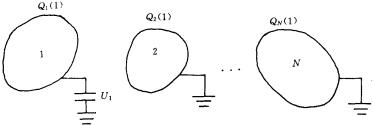
　　如图所示，使导体1具有电势 ，其余各导体电势均为零，在此情况下，导体1充电后电量为 （1），其余导体上的感应电荷电量分别为 （1），…， （1），这N个电量都是由 所引起，故它们与 成正比，即：

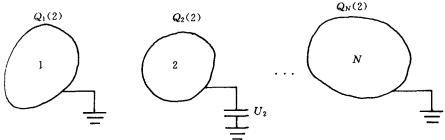
　　再使导体2具有电势 ，其余各导体电势均为零，如图所示。由于导体2具有电势 ，使这N个导体分别具有电量 （2）， （2），…， （2），它们之间的关系为：

依此类推，直到使第N个导体具有电势 ，其余导体电势为零，N个导体上电量分别是 ，并得出下列关系：

当使N个导体同时分别具有电势 时，每个导体上的电量应为：

以上N个等式可用通式表示为：

          （1）

式中 叫电容系数，它的物理意义是第j个导体具有单位电势时在第i个导体上感应电荷的电量，它的大小与导体系中各导体的大小、形状、相对位置及周围介质的性质有关，与导体系的电量与电势无关。应用静电场的格林互易定理，可以证明 有一个重要性质．即：

                              （2）

（2）式表明，导体系中第j个导体具有单位电势在第i个导体上产生的感应电荷，与第i个导体具有单位电势在第j个导体上产生的感应电荷相等。

　　下面我们回到当电容器分别带有电荷 和 （ ），电容器的电容仍可用 定义，Q是指要使电容器两板电势相等时，从一个极板向另一个极板转移的电量， 是电量转移之前两极板之间原有电势差结论的证明上。

　　显然，在电量Q转移之前，根据（1）式有如下关系：

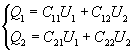                （3）

　　电量Q转移之后，有以下关系：

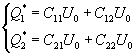           （4）

（4）式中 、 和 是Q转移后两极板所带的电量及共同的电势。

　　根据电荷守恒定律，Q转移前后电容器所带有的总电量保持不变，即：

          （5）

　　再根据（2）式有：

                    （6）

　　由（3）～（6）四式联立，可解得：

                                     （7）

　　令：

        （8）

         （9）

　　则（7）式可写成：

              （10）

　　由（8）式可看出，Q是极板1上电荷的减少量，也是极板2上电荷的增加量，因而Q是两极板之间转移的电量。 乃是两极板之间原有的电势差。由（9）式可看出，当两极板的大小、形状和相对位置以及周围的介质不变时， 、 、 都保持不变，也就是C保持不变，C就叫做电容器的电容。可见Q与 是成正比的。

　　这里所说的电容器电容的定义式与一般书中所说的定义式是一致的，后者仅是前者的特例，前者更具有普遍意义。对此，举例说明如下：

例1：

　　平行板电容器。分两种情况讨论。

　　（1）有一个极板接地的情况。如图所示，容易证明，当两极板很靠近且无外部导体和带电体的影响时，两极板相对的内侧面带有等量异号电荷 与－ ，外侧面没有电荷分布。

　　当用导线连接两极板后，它们的电势均为零， 与－ 完全中和，它们的电量也都是零，即：

          （11）

　　因而电量的转移为：

        （12）

　　则（l0）式变为：

             （13）

　　 这表明电容器的电容C等于每个极板所带电量与两极板间的电势差之比，这样自然就回到了一般教科书中的定义式。

　　（2）两极板都不接地的情况。如 图所示，两极板的内侧电荷面密度分别为 、 ，外侧电荷面密度分别为 、 ，两极板侧面积均为S，用电磁学知识即可求得：

    （14）

　　用导线连接两极板后，因为两极板的几何性质完全一样，静电平衡时它们所带的电量相等，即：

    （15）

　　所以转移的电量为：

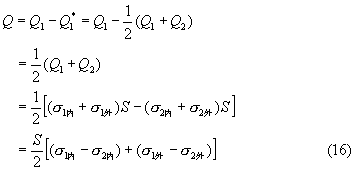
　　根据（l4）式，则（16）式可变为：

　　可见，尽管两极板所带的电量不同，但它们的内侧面所带电荷是等量异号的，而且转移的也就是这部分电量。现在（10）式可变为：

     （18）

　　注意， 是两极板内侧面上的电量，不是每个极板上的总电量，电容为每个极板内侧面所带的电量与两极板间电势差之比。

　　由于两极板完全一样，根据对称性，有：

     （19）

　　把（19）式代入（9）式可得：

    （20）

　　当一个极板接地时，（3）式变为：

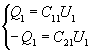      （21）

　　由（21）式和（2）式可得出：

      （22）

　　将（22）式代入（20）式，最后得到：

      （23）

例2：

　　球电容器。如图所示，内外球壳半径分别为 与 ，各带电荷分别为 与 ，此时两球壳的电势差为：

　　用导线将内外球壳相连时，内球壳上的电荷将全部转移到外球壳的表面上，故转移的电量为：

      （25）

　　故（10）式此时可变为：

　　显然，（26）式与普通物理书中的结果相同。