设为首页
设为首页
 加入收藏
加入收藏
扩展资料
《墨经》中有关杠杆的知识
墨家是我国古代的一个学派,这个学派的成员多来自生产第一线,有丰富的技术知识和刻苦的钻研精神,研究科学技术的风气特别盛,有不少创造发明,对后世的科学发展起着积极作用.墨翟是战国初期鲁国人,是墨家创始人.《墨经》是墨家学者的集体创作.
《墨经》一书中有两条专门记载杠杆的原理.一条说:“衡木,加重焉而不挠,极胜重也;右校交绳,无加焉而挠,极不胜重也.”意思是说:在横杆的一端加上重物而不致发生偏转(“挠”),那一定是预先固定有石块的一端(即“极”)的转矩,足以胜任重物一端的转矩.此时如果把支点(“交绳”)移近“极”端,即不必另加重物也可以使杠杆偏转,这时是“极”的转矩不能胜任重物的转矩.
另外一条是专门从杠杆原理讨论天平与杆秤的.条文是这样的:“衡木:加重于其一旁必捶——重相若也.相衡:则本短标长,两加焉,重相若,则标必下——标得权也.”这段文字上半是说天平的.意思是:天平横梁的一臂加重物,另一臂必得加砝码(“必捶”),两者必须等重,才能平衡.下半是说杆秤的.意思是说:杆秤的提纽到重物的一臂(“本”)比较短,提纽到秤锤的臂(“标”)比较长,如果两边等重,秤锤一过必下落.为什么呢?因为种锤对“标”一边的作用过大了.
这两条对杠杆的平衡条件说得很全面:有等臂的,有不等臂的;有改变两端重力使它转动的,也有改变两端长度使它转动的.这样的记载,在世界物理学史上都是非常有价值的.
扩展资料
杆秤的部件及原理
1、零刻度(即定盘星)
如图5示:秤杆上提绳的O点为支点,由于支点不在秤杆(包括秤钩)的重心上,在不称物体时,手提绳,秤杆不能平衡于水平位置,此时必须把秤砣挂在适当的位置C点上,才能使杠杆平衡.C点就是杆秤的零刻度,通常叫做定盘星.
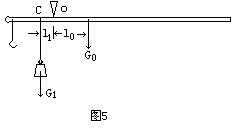
设杆重为G0,砣重为G1,重心到支点的距离为l0,C点到支点的距离为l1.根据杠杆的平衡条件,有G0·l0=G1·l1
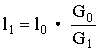
这样定盘星C的位置就可以确定.
2、确定杆秤的刻度
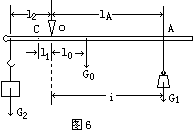
在称物重时,将物体G2挂在秤钩上,若保持秤杆平衡在水平位置上,需要把秤砣移到A点,如图6所示.
根据杠杆的平衡条件,则有 G2·l2=G1lA+G0·l0
因为不称物体时G0·l0=G1l1
所以G2·l2=G1lA+G1·l1=G1(lA+l1)
又因为l=lA+l1
所以G2·l2=G1·l
即 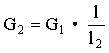
由上式可以看出,由于 ![]() 对同一杆秤是不变的,G2与l成正比,所以秤杆上从定盘星开始表示尺数的刻度是均匀的,用等分法可以确定杆秤的刻度.
对同一杆秤是不变的,G2与l成正比,所以秤杆上从定盘星开始表示尺数的刻度是均匀的,用等分法可以确定杆秤的刻度.
3、扩大杆秤的量程
某杆秤最多可以称5千克的物体,能否对秤稍加修改,扩大它的量程呢?根据杠杆的平衡条件,改变支点的位置(即在靠近钩子处再加上一个提绳),这样又可以用上面的方法刻度出新的刻度来,一般的杆秤都备有两个提纽,两套刻度,大大增加了它的称量范围.
扩展资料
简易杠杆实验装置的制作
在没有课本上杠杆实验器材的情况下,可用如图所示的简单器材来做这个实验,用轻质木条或刻度尺做杠杆,把它支放在三棱木块的棱上,也可用方木块压放在湿粘土上,以向上的棱边作为支放杠杆的棱边;用一些相同的硬币作为砝码(每枚硬币的平均质量可用天平测出)。实验时,先让木条或刻度尺在三棱木块的棱上平衡,然后根据课本上的步骤放置硬币进行杠杆平衡的实验。根据实验数据,可以粗略地得出杠杆平衡条件。

扩展资料
人身上的杠杆
在人体生理卫生课上已经学过,人身上有206块骨,其中有许多起着杠杆作用,当然这些起杠杆作用的骨不可能自动地绕支点转动,必须受到动力的作用,这种动力来自附着在它上面的肌肉.
肌肉靠坚韧的肌健附着在骨上.例如肱二头肌上端肌腱附着在肩胛骨上,下端肌腱附着在桡骨上(如图),肱三头肌上端有肌腱分别附着在肩胛骨和肱骨上,下端附着在尺骨上.
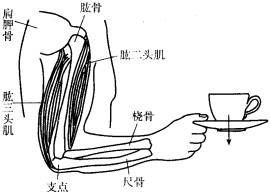
人前臂的动作最容易看清是个杠杆了,它的支点在肘关节.当肱二头肌收缩、肱三头肌松弛时,前臂向上转,引起曲肘动作;而当肱三头肌收缩、肱二头肌松弛时,前臂向下转,引起伸肘动作.从上图很容易看出,前臂是个费力杠杆,但是肽二头肌只要缩短一点就可以使手移动相当大的距离.可见,费了力,但省了距离.
如图是跑动时腿部肌肉示意图,为了画面简单容易看清,右腿没有画出臀大肌、股四头肌,左腿没有画出髂腰肌①、股二头肌.当右腿向前跨步时,是右腿的髂腰肌收缩、臀大肌松弛,使右大腿抬起;股四头肌松弛,股二头肌收缩,使右膝弯曲.这时候,左腿由于它的髂腰肌松弛,臀大肌收缩,股四头肌收缩,股二头肌松弛,而伸直.