 设为首页
设为首页
 加入收藏
加入收藏
扩展资料
功和能概念的科学定义
功与能是物理学中极其重要的基本概念,也是教师感到不易讲授的概念.有的书上说“功是物体作功的本领”,又有的书上说“功的储藏就是能”,还有的书上说“能是物体运动的度量”.这些说法是否都对呢?究竟什么是功?什么是能?它们之间又有什么联系?什么区别呢?
上面诸问题都牵涉到如何对功和能的概念作出科学的定义.
1.什么是功
“功”是由“工作”一词发展起来的物理量.在日常用语中,“工作”的意思范围很广,也很笼统.但是,在物理学中,功却有特定的含义.
福里斯在他的专著《普通物理学》中关于功的概念是这样引出的:“在我们周围的环境中,我们接触的都是一些彼此之间以某种力(弹性力、万有引力、摩擦力以及其他各种力)互相作用着的物体.所以,在这种情况下,物体的位置改变,只有在力的作用下才能实现.因此,自然就有表明力使物体移动的作用特性的必要性.在力学中,作为这种特性,所取的是这样一个量:沿移动方向的分力和这分力的作用点移动的距离愈大,这个量也愈大.这个量叫做功.”这一段话的前一半说明功的概念是如何产生的.它包含着两个重要因素:其一就是物体与物体之间的相互作用;其二就是在相互作用之下物体位置改变的过程所具有的一个共同的特性,这一特性就是功.这两个重要因素也就是现在我们一般的物理书中所强调的作功的两个要素.这一段话的后一半则叙述功的概念的数量是怎样测定的,即![]() ,其中s表示力的作用点移动的距离(即移位的大小),
,其中s表示力的作用点移动的距离(即移位的大小),![]() 表示力在位移方向的分力.我们认为福里斯对功下的定义是科学的,它跟我们现在大多数物理书中把功定义为
表示力在位移方向的分力.我们认为福里斯对功下的定义是科学的,它跟我们现在大多数物理书中把功定义为![]() 是一致的.
是一致的.
以上功的定义之所以科学,并不是因为它比较简洁,应用方便,而是因为这样的定义反映了“同时被许多其他物理量所描述的大量真实过程的特性”(此问题留待功与能的联系和区别一节再详细论述).
根据功的定义式![]() 可知,功是一个标量.功的大小除了决定于力、力作用点位移的大小外,还与力F和位移s之间的夹角
可知,功是一个标量.功的大小除了决定于力、力作用点位移的大小外,还与力F和位移s之间的夹角![]() 的大小有关.当
的大小有关.当![]() 时,则
时,则![]() ,表示力对物体作了正功,力是推动物体运动的动力;当
,表示力对物体作了正功,力是推动物体运动的动力;当![]() 时,则
时,则![]() ,表示力对物体做了负功,力是物体运动的阻力,此情形往往说成物体克服阻力做了功;当
,表示力对物体做了负功,力是物体运动的阻力,此情形往往说成物体克服阻力做了功;当![]() 时,则
时,则![]() ,表示力对物体没有做功,但是注意这种情况与物体在力作用下并没有发生位移而称之没有做功的情况是不同的.这里所称的力没有作功,是因为力的方向始终垂直干作用点位移的方向所致.譬如,作匀速圆周运动的向心力;人提着重物在水平面上匀速行走等,尽管有力,也有位移存在,即具有所谓作功的两个重要因素,但因为这里的力与力作用点的位移始终垂直,故力对物体仍没有作功.这决不是哪个人服气不服气的事,从下面功能关系中可知这是一个科学规律!功的国际单位和法定计量单位是焦耳.
,表示力对物体没有做功,但是注意这种情况与物体在力作用下并没有发生位移而称之没有做功的情况是不同的.这里所称的力没有作功,是因为力的方向始终垂直干作用点位移的方向所致.譬如,作匀速圆周运动的向心力;人提着重物在水平面上匀速行走等,尽管有力,也有位移存在,即具有所谓作功的两个重要因素,但因为这里的力与力作用点的位移始终垂直,故力对物体仍没有作功.这决不是哪个人服气不服气的事,从下面功能关系中可知这是一个科学规律!功的国际单位和法定计量单位是焦耳.
2.什么叫能
关于能概念的精确物理定义是在1887年由普朗克所阐明的.
当一物体的运动状态发生变化时,这一变化可以用功来量度,但如果是由于其他的作用(热、电、磁、辐射、化学等等)所引起的,则也可以用等值的机械功来度量,因为各种运动形态可以相互转变.这样便有了比较任何一种外界作用的方法.其次,由能量守恒与转换定律所概括的大量实验事实表明,当一物体(系)由某一状态经过不同的方式及过程改变到另一状态时,在这些不同的方式过程中所消耗的功或等值机械功总是一般多的.因此,就可以用一个物理量E来表示物体(系)本身的特征,E就是物体(系)的能.当物体(系)由某一状态(Ⅰ)改变到另一状态(Ⅱ)时,E的改变则决定于等值的机械功,并用以表示外界作用,即:
![]() (1)
(1)
式中 ![]() 与
与 ![]() 分别表示物体(系)在状态(Ⅰ)和状态(Ⅱ)的能,
分别表示物体(系)在状态(Ⅰ)和状态(Ⅱ)的能,![]() 表示使此物体(系)从状态(Ⅰ)改变到(Ⅱ)的所有外界的等值机械功的总和.譬如,大家都熟知的热力学第一定律:
表示使此物体(系)从状态(Ⅰ)改变到(Ⅱ)的所有外界的等值机械功的总和.譬如,大家都熟知的热力学第一定律:
![]()
此式其实就是(1)式的具体体现,只需把热力学第一定律改写成:
![]()
就可反映出来.与(1)式对照,等式左边与(1)式右边相当,![]() 是外界供给物体(系)的热量,所谓的等值功,
是外界供给物体(系)的热量,所谓的等值功,![]() 就是外界对物体(系)所做的机械功;等式右边与(1)式左边相当,即所谓物体(系)能量(这里指内能)的变化.
就是外界对物体(系)所做的机械功;等式右边与(1)式左边相当,即所谓物体(系)能量(这里指内能)的变化.
物体(系)的状态是用不同的物理量即所谓的“参量”来描述的,物理量E也必然是与这些物理量有联系的,即E是相关的参数函数.不仅如此,既然大量的实验事实都表明了当物体(系)从某一状态由木同的方式及过程改变到另一状态时所消耗的功或等值机械功总是一般多的.这也等于说,当物体(系)经过一系列的改变过程又回复到原始状态时,这一循环过程中,外界对物体(系)所作的功和等值机械功的总和总是等于零的(即第一类永动机不可能原理),那么,E必然是相关参量的单值函数.即由(1)式规定的能的概念确有意义.
通过以上论述,我们可对能的概念下一个精确的定义:物体(系)的能是描述它的运动状态的一个特殊的物理量,这一物理量是物体(系)状态的单值函数,是物体运动的一般量度.显然,能是一个标量,它的单位同功的单位相同.
中学物理中说:“能是做功的本领”,这种说法显然也是正确的,可以说是以较通俗的语言刻划出能概念的基本内容.由(1)式可以看出,当外界对物体(系)作负功时,![]() ,因而
,因而 ![]() <
< ![]() ,即物体(系)的能在减小.这时物体(系)对外做了正功.因此,如果取
,即物体(系)的能在减小.这时物体(系)对外做了正功.因此,如果取
![]() ,则立即可以得出物体(系)对外界所做的功正好度量了物体(系)在状态(Ⅰ)之下所具有的能.这说明的确可以把能理解成作功的本领.例如,以速度v运动的物体转变到速度为零时,它对外界所做的功正好等于
,则立即可以得出物体(系)对外界所做的功正好度量了物体(系)在状态(Ⅰ)之下所具有的能.这说明的确可以把能理解成作功的本领.例如,以速度v运动的物体转变到速度为零时,它对外界所做的功正好等于![]() .因此,
.因此,![]() 确是表示物体在速度为v的运动状态下所具有的作功本领,今天我们称之为“动能”.不过,“能是做功的本领”这种说法也有着明显缺陷.其一,(1)式规定的能只是两个状态的能的差值,它们还相差一个常数,这就是我们平常所称的零点能的选择问题.只有零点能(参考点)选定后,才能精确地给出物体的能值,否则只是一个相对量.其二,“能是做功的本领”这一说法并没有把能的概念更本质、更完整的内涵及意义表示出来,只是考虑到中学生的认识水平和接受能力的限度才认为它是正确的.
确是表示物体在速度为v的运动状态下所具有的作功本领,今天我们称之为“动能”.不过,“能是做功的本领”这种说法也有着明显缺陷.其一,(1)式规定的能只是两个状态的能的差值,它们还相差一个常数,这就是我们平常所称的零点能的选择问题.只有零点能(参考点)选定后,才能精确地给出物体的能值,否则只是一个相对量.其二,“能是做功的本领”这一说法并没有把能的概念更本质、更完整的内涵及意义表示出来,只是考虑到中学生的认识水平和接受能力的限度才认为它是正确的.
3.功与能的联系及区别
从以上我们对能的概念的阐述可以看出,功与能这两个概念实际上有着不可分割的联系,为能更深刻地认识这种关系,我们再以一个机械运动实例来说明.
 如图所示,一个质量为m的物体放在光滑的水平桌面上,其初速度为
如图所示,一个质量为m的物体放在光滑的水平桌面上,其初速度为![]() ,受到一恒力F的作用,力的方向与物体位移的方向成
,受到一恒力F的作用,力的方向与物体位移的方向成![]() 角.物体在此力作用下沿水平面作匀加速直线运动.如果物体发生的位移为s时速度为
角.物体在此力作用下沿水平面作匀加速直线运动.如果物体发生的位移为s时速度为![]() ,则由匀加速直线运动的公式可知.物体的加速度是:
,则由匀加速直线运动的公式可知.物体的加速度是:
![]()
如果把这个式子代入牛顿第二运动定律表示式中,就可以得到;
![]()
两边乘以位移大小s,就得到:
![]()
根据前述功的定义可知,上式左边就是恒力F对物体所做的功,即:
![]()
上式右边的两项均有相同的形式,即![]() .显然,它是描述物体运动状态的一个物理量,即能,而
.显然,它是描述物体运动状态的一个物理量,即能,而![]() 便是物体由初始状态变到终止状态时的能量之差(这里不考虑相对论效应).由此得出结论:恒力F对物体所作的功等于物体动能的增量.这就是所谓动能定理,它是被大量实验所证实的客观规律.设想,如功的定义不是如前所述,不能得出这一结论.可见,前述功的定义确是一个科学定义.
便是物体由初始状态变到终止状态时的能量之差(这里不考虑相对论效应).由此得出结论:恒力F对物体所作的功等于物体动能的增量.这就是所谓动能定理,它是被大量实验所证实的客观规律.设想,如功的定义不是如前所述,不能得出这一结论.可见,前述功的定义确是一个科学定义.
概括地说,能是描述物体运动状态的物理量,它是物体运动状态的单值函数(简称态函数).而功则是在物体与外界相互作用的情况下,物体运动状态改变的量度,或可直接说功是物体能量变化的量度.功与物体状态的具体变化过程有关,是一个过程量,并不是状态函数.所以,只能说物体具有多少能量,而决不能说物体具有多少功.根据物理教学的通俗性与可接受性原则,对待中学生可以这样比喻:功和能的关系犹如“雨”和“水”的关系.“雨滴”在从天空落到河面这段过程中,从来不称它为“水”,尽管雨滴的化学成份是![]() .但雨滴一落到河面,我们便称之为“水”,而不再称之为“雨滴”了.相仿,受力物体在运动状态变化过程中,外力时刻在对物体作功时,这种过程中的功我们也从来不称之为“能”,仅在描述物体的特定状态时才用“能”这个概念.当然,能的变化量可用过程中的功值来量度.尽管这个比喻不怎么确切,但多少能说明一些问题.
.但雨滴一落到河面,我们便称之为“水”,而不再称之为“雨滴”了.相仿,受力物体在运动状态变化过程中,外力时刻在对物体作功时,这种过程中的功我们也从来不称之为“能”,仅在描述物体的特定状态时才用“能”这个概念.当然,能的变化量可用过程中的功值来量度.尽管这个比喻不怎么确切,但多少能说明一些问题.
扩展资料
关于功的定义的研究
关于功的定义,各种课本的说法不同.原高中物理课本是这样说的:“功的大小等于力和受力作用的物体在力的方向上所通过的路程的乘积.如果用F代表力,用s代表物体在力的方向上通过的距离,用W代表力所做的功,那么![]() .”新编高中物理课本没有给出功的完整表述,初中课本的说法与此相同.一般普通物理的说法是:“功的数值等于力F、力的作用点的位移s及力与位移的方向间的夹角的余弦的乘积,即
.”新编高中物理课本没有给出功的完整表述,初中课本的说法与此相同.一般普通物理的说法是:“功的数值等于力F、力的作用点的位移s及力与位移的方向间的夹角的余弦的乘积,即![]() .”总的来说,功的各种叙述的主要区别在于:有的用“物体的位移”(原高中课本用距离,严格来说应是位移,对作单向的直线运动的质点来说,它的位移数值和路程相等),有的用“力的作用点的位移”.一般来说,物体的位移和力的作用点的位移是有区别的.通过下面的例子分析,我们将看到:用力和物体的位移的乘积来定义功是不恰当的;用力和力的作用点的位移的乘积来定义功才符合实际.
.”总的来说,功的各种叙述的主要区别在于:有的用“物体的位移”(原高中课本用距离,严格来说应是位移,对作单向的直线运动的质点来说,它的位移数值和路程相等),有的用“力的作用点的位移”.一般来说,物体的位移和力的作用点的位移是有区别的.通过下面的例子分析,我们将看到:用力和物体的位移的乘积来定义功是不恰当的;用力和力的作用点的位移的乘积来定义功才符合实际.
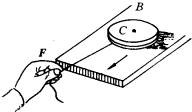 例如,一质量为m,半径为R的匀质圆盘平放在光滑的水平面上,盘面也绝对光滑.若在圆盘的边上作用一个力F,设力F的作用线通过圆盘质心C(见图).当圆盘在力F的作用下移动s时(所经历时间为t),F所做的功
例如,一质量为m,半径为R的匀质圆盘平放在光滑的水平面上,盘面也绝对光滑.若在圆盘的边上作用一个力F,设力F的作用线通过圆盘质心C(见图).当圆盘在力F的作用下移动s时(所经历时间为t),F所做的功![]() .将
.将![]() .(质心运动定律)分别代入功的表达式则得:
.(质心运动定律)分别代入功的表达式则得:
![]()
 (这里
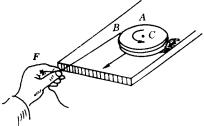
(这里![]() 为质心C在t时刻的速度大小).现以相同的力F作用在圆盘的边缘切向上(用一忽略质量的细线绕在盘的边缘上,用力F拉线),如图所示,并使圆盘同样移动人可证所经历时间仍是t),此时,如按“物体的位移”来计算功,则F所做的功仍是
为质心C在t时刻的速度大小).现以相同的力F作用在圆盘的边缘切向上(用一忽略质量的细线绕在盘的边缘上,用力F拉线),如图所示,并使圆盘同样移动人可证所经历时间仍是t),此时,如按“物体的位移”来计算功,则F所做的功仍是![]() .其实,由于力F未通过盘质心C,圆盘既有平动又有绕质心C的转动,作为圆盘的力的瞬时作用点,除参与质心的平动外,还要参与绕质心的转动,因而力的作用点的位移应是质心的位移和力的瞬时作用点绕质心转动的位移之和.在dt时间内,上述两位移分别为:
.其实,由于力F未通过盘质心C,圆盘既有平动又有绕质心C的转动,作为圆盘的力的瞬时作用点,除参与质心的平动外,还要参与绕质心的转动,因而力的作用点的位移应是质心的位移和力的瞬时作用点绕质心转动的位移之和.在dt时间内,上述两位移分别为:
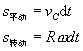
且方向一致.所以作用点的合位移为:
![]()
如按力的作用点的位移来计算功,则在dt时间内力F所做的功为![]() .因为F是恒力,所以圆盘质心作匀加速运动,转动也是匀角加速的.于是,在质心移动s的有限时间t内,力F所做的总功为:
.因为F是恒力,所以圆盘质心作匀加速运动,转动也是匀角加速的.于是,在质心移动s的有限时间t内,力F所做的总功为:
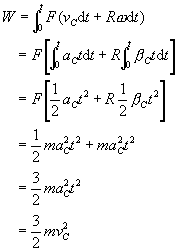
(其中用到质定运动定律![]() ,转动定律
,转动定律![]() ).显然,在这里,按照“物体的位移”算得的功与按照“力的作用点的位移”算得的功是不同的.何种正确?就须进一步验证.
).显然,在这里,按照“物体的位移”算得的功与按照“力的作用点的位移”算得的功是不同的.何种正确?就须进一步验证.
下面就根据动能定理来验证.
如上所述,在边缘恒力F作用下,匀质圆盘既有质心的平动又有绕质心的转动.设F作用时间为t,则到t时刻圆盘就有确定的运动状态,从而就有着确定的动能,根据动能定理,此时圆盘的动能值就应等于t时间内恒力F所做的功值.
圆盘的平动动能:
![]() (1)
(1)
圆盘的转动动能:
![]() (2)
(2)
![]() ,I为圆盘对通过质心的垂直轴的转动惯量,
,I为圆盘对通过质心的垂直轴的转动惯量,![]() 为圆盘在t时刻绕质心的转动角速度.
为圆盘在t时刻绕质心的转动角速度.
因为:

(![]() 是盘绕质心转动的角加速度).因为:
是盘绕质心转动的角加速度).因为:
![]()
于是:
![]()
代入(2)式得:
![]()
最后得圆盘t时刻的总动能为:
![]()
与上述按“力的作用点位移”算得的功值相等,故按“力的作用点的位移”计算功值是符合动能定理的,正确的.事实上,作用在圆盘边缘的切向恒力F在时间t内所做的功一部分用来增加盘的平动动能![]() ,另一部分是用来增加盘的转动动能
,另一部分是用来增加盘的转动动能![]() 的.显然,如果仅考虑盘的质心位移,而不从力的作用点的位移来考虑是得不到正确结果的.
的.显然,如果仅考虑盘的质心位移,而不从力的作用点的位移来考虑是得不到正确结果的.
 上述的例子只是抬物体的转动情况,事实上,即使对于没有转动的物体,有时也必须从“力的作用点的位移”来计算功,才能得出正确的结果.如图所示,用一质量不计的弹性系数为k的弹簧连接一重物M.若用力F将弹簧拉长x,但重物因受阻力作用本动.在此问题中,若按“物体的位移”来算功,由于物体位移为零,则力F所做功为零,显然是错误的,只有从“力的作用点的位移”来计算功才能得到
上述的例子只是抬物体的转动情况,事实上,即使对于没有转动的物体,有时也必须从“力的作用点的位移”来计算功,才能得出正确的结果.如图所示,用一质量不计的弹性系数为k的弹簧连接一重物M.若用力F将弹簧拉长x,但重物因受阻力作用本动.在此问题中,若按“物体的位移”来算功,由于物体位移为零,则力F所做功为零,显然是错误的,只有从“力的作用点的位移”来计算功才能得到![]() 这个正确的结果.
这个正确的结果.
由以上分析可知,功的定义应为:力和力的作用点在力的方向上通过的位移的乘积.现行课本中用了物体移动的位移(初中是路程),用“路程”,这对初中学生来说,是比较容易接受的,也是可取的.但是,在高中物理中应指出是“力的作用点的位移”.