第十一节 有理数的混合运算　

扩展资料

( )，[ ]，{ }──小括号，中括号，大括号

　　大家都知道，当一个算式里含有加、减、乘、除、乘方等几种运算时，通常是按先算乘方、再算乘除、最后算加减的顺序进行．

　　但是在计算中，为了某种特殊的约定，需要改变常规的运算顺序时，就要把提前演算的部分，添上一个括号．

　　请看下面的两个算式：

　　　　a＋b·c， (1)

　　　　(a+b)·c． (2)

　　在(1)式中，要先算乘法，再算加法．

　　在(2)式中，要先算括号里的加法，再算乘法．

　　其中(a+b)是约定要提前演算的部分，所以添加了一个括号，这是括号产生的历史背景．

　　常见的括号，有下面三种形式：

　　( )叫做小括号，又称为圆括号．早在1544年就采用了．在小括号出现之前，历史上曾用括线“──”代替过它，例如计算：

　　这里的括线和小括号“( )”有着同样的功能．

　　[ ]叫做中括号，又称方括号．17世纪，英国数学家华里士在计算时最先采用了它．

　　{ }叫做大括号，又称花括号．它是1593年由数学家韦达首先创用的．

　　这三种括号中，以小括号应用的范围最为广泛．例如，在表示一个负数的乘方时，要把负数用( )括起来，把乘方的次数写在小括号的右肩上．比如“-5的平方”这句话，要写成(-5)2，如果粗心大意写成-52，就是错误的了．

　　也许有人问：当一个算式里有多种括号时，应怎样运算呢？

　　这时要注意它们运算的顺序：先去小括号，再去中括号，最后脱掉大括号．例如：

　　

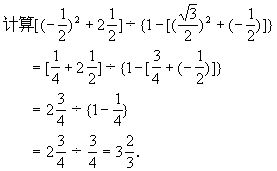
摘自《数学符号史话》

返回页首