第一节 分式

扩展资料

怎样正确理解分式概念？

　　[解答] 由于分式的概念是在与分数类比引入分式概念的基础上，通过实际问题建立起来的，所以对比分式与分数概念的异同，可以加深对分式概念的正确理解．

　　(1)两个整数相除可以表示成分数的形式．如
　　

　　两个整式相除可以表示成分式的形式，如
　　

　　一般地，用A、B表示两个整式，就可以表示成的形式。即分式就是两个整式相除的商，其中分母是除式，分子是被除式，而分数线可以理解为除号，且含有括号的作用，如的商写作不必写成.

　　(2)分数的分子和分母都是具体数值(不含字母)．

　　分式的分子中可以含字母，也可以不含字母，即式子中，A既可含字母，也可以不含字母，但分式的分母中必须含有字母，即式子中，B中必须含有字母，这就是区别整式与分式的关键，如在式子

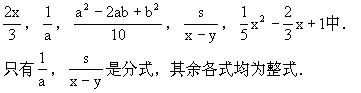
　　(3)因为“零不能作除数”，所以无论是分数还是分式，分母都不能是零．

　　由于分数的分母是具体数值，其值是否为零一目了然，而分式的分母中含有字母，其值是否为零就必须分析、讨论分母中所含字母的取值范围，以避免因分母的代数式的值为零而使分式失去意义．如

　　在分式中，分子中的字母y可以取任意数值，而分母中的字母x只能取除去±1以外的任意数值．

　　综上所述，用A、B表示两个整式，就可以表示成的形式，如果B中含有字母，式子就叫做分式，其中。

返回页首