第一节正弦和余弦

作者：未知来源：中央电教馆时间：2006/4/8 18:03:14阅读：nyq

字号：小|大

例说数学解题的思维过程

陕西师范大学数学系罗增儒

　　在数学教学中暴露思维过程早就引起了人们的关注．暴露概念的形成过程，暴露命题的发现过程，暴露证明的探究过程等，包括暴露这些过程中犯错误的真实活动．但是，这种暴露大多停留在可见事实的陈述上，内在思维性质的细致揭示不多，也常常进行到思路初步打通、结论初步得出时就停了下来．本文想从解题分析的角度提供一个简单例子，展示内在的思维过程，并在证明得出之后仍继续进行下去．先给出题目：

　　两直线被第三条直线所截，有外错角相等，则两直线平行．

　　1．浮现数学表象

　　通过认真阅读，我们接收到题目所提供的信息，首先在脑子里出现了一个图形（几何型表象），与这个图形相伴随的是一个问题（代数型表象）：由数量关系去确定位置关系．

　　在问题的牵引下，思维的齿轮开始启动，有3个展开的起点．

　　（1）由图形表象，我们回想起“三线八角”基本图形，回想起与此图形有关的命题，如两直线被第三条直线所截，有：

　　1）同位角相等两直线平行；

　　2）内错角相等两直线平行．

　　这些命题的附图，在我们脑海里逐幅浮现出来．

　　（2）由条件（数量关系）所唤起的问题有：

　　1）由角的相等关系能得出什么？进而问

　　2）图1中有与相等的角吗？

　　3）图1中有与相等的角吗？

　　一开始，“由条件能推出什么”是一道开放性问题，我们不知道该往哪些地方推进，但随着对结论思考的深化，会慢慢明朗起来．

　　（3）由结论（位置关系）所唤起的问题有：得出直线平行需要什么条件？题目提供了这样的条件没有？如果不是直接提供，那么间接提供没有？……

　　由此激活了记忆储存中的相关知识，并又激活更多的记忆储存（扩散）：

　　1）同位角（内错角）相等，则两直线平行；进而问

　　2）什么是同位角（内错角）？图1中有同位角（内错角）吗？有相等的同位角（内错角）吗？

　　3）已知条件的相等角能导出“同位角（内错角）相等”吗？

　　……

　　这是表象的一个有序深化过程．

　　2．产生数学直感

　　上述三方面的思考，促使我们更专注于图形，图中有3条直线，8个角，8条射线，1条线段，其中哪些信息对于我们解题是有用的，哪些是多余的呢？（这相当于一道条件过剩、结论发散的开放题）当然，一开始我们并不清楚，但是目标意识驱使我们去考虑角的关系，因为课本中两条直线平行的判定均与角有关，而已知条件又给出了等角．所以，我们的思考逐渐集中到：从图形中找同位角（或内错角），找相等的角，找相等的同位角（或内错角）．

　　这时，伴随着问题的需要，图1被分解出一系列的部分图形（图2中实线图），并凸现在我们的眼前：

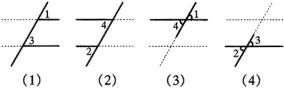
　　（1）有与成同位角的角吗？图2–（1）出现，进而问，与会相等吗？

　　（2）有与成同位角的角吗？图2–（2）出现，进而问，与会相等吗？

　　（3）与（或）成内错角关系的角，图1找不到．

　　（4）与相等的角除外，还有它的对顶角（图2–（3））；与相等的角除外，还有它的对顶角（图2–（4））．

　　……

　　于是，对图1的感知，出现了图3的右方图形．

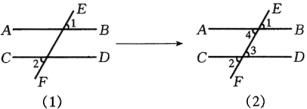
　　我们认为，从图1的8个角中找出的对顶角（或的对项角），是解题的重大进展，它能为图形各部分数学关系的沟通起桥梁作用．

　　3．展开数学想象

　　对具体形象的感知和判别，使我们看到与成对项角（图2–（4））是相等的，而又与成同位角（图2–（1）），这促使我们思考与会不会相等，也促使我们将已有的表象

　　与（或），产生新的联结（有逻辑思维的推动），得

　　（或或），

　　从而产生新的表象

　　．

　　于是，在数量关系与位置关系之间，在空旷而缺少联系的画面上（见图1），添上了两个数量关系，：

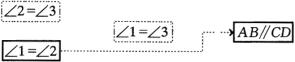
　　将它们组成和谐的逻辑结构，便得出证明．

　　4．给出逻辑证明

　　证明1：

　　证明2：

　　证明3：

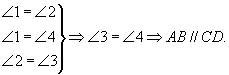
　　这些证明是抽象思维的过程，表达得干净、简洁而严密．而获得这些结果的过程却是历经“表象—直感—想象”的形象思维过程，在得出之前，四个角、、、之间的关系是一个条件与结论都发散的开放题．为了与简捷的逻辑证明相对照，我们将思考过程（证明1）图示如下：

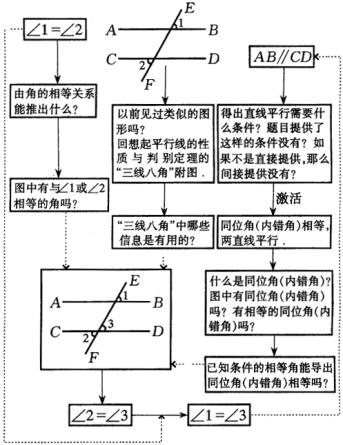
　　5．反思解题过程

　　上述解题的过程，把“题”作为考察的对象，把“解”作为研究的目标．我们推崇“解题分析”，是希望解题研究不要停留在这一阶段上，继续把上述解题活动（包括问题和解）作为研究对象，探究解题规律，学会怎样解题（基本任务），具体研究的方法是分析解题过程．

　　事实上，给出的证明也是一个思维过程，也需要我们去暴露，并且这种暴露比前一阶段的暴露有更高的层次、需要更强的自觉性，是培养思维深刻性与批判性的极好途径．我们一再说过，解题教学缺少这一阶段是进宝山而空还．而把这一阶段停留在检验、回顾、寻找一题多解、作出若干推广的常识层面上，则是一种损失与浪费．让我们对证明1的书写作出具体结构的分析．

　　（1）首先，我们将证明1分解为三个步骤．

　　第1步：从图形中看出与成对项角，并得出．这是由位置关系推出数量关系的过程．

　　第2步：把另一已知条件用上，将两个等式、结合起来，得出．这是由数量关系推出新数量关系的过程．

　　第3步：从图形中看出与为同位角，其相等可得出．这是由数量关系推出位置关系的过程．

　　示意为：

　　（2）其次，根据上面的整体分解，可将证明1的书写加以充实：

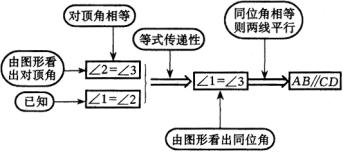
　　（3）由于这个图形已经显示出，解题中用到了哪些知识（或方法），先用哪些后用哪些，哪个与哪个作了配合．所以，只须将其再作充实（图7），便可更自觉、也更直观地看到，解题过程是这样一个“三位一体”的工作：有用捕捉、有关提取、有效组合：

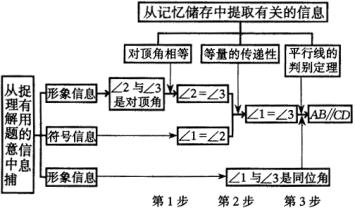
　　1）从理解题意中捕捉有用的信息．

　　包括从题目的叙述及题目的附图两方面去充分理解题意．从图7可见，这共有3条信息．

　　（a）从题目的文字叙述中获取“符号信息”．

　　　　　　　　　　 ①

　　（b）从题目的图形中获取“形象信息”．

　　与为同位角，　　　②

　　与为对顶角，　　　③

　　2）从记忆储存中提取有关的信息．

　　这是一批被解题需要激活的知识，并随着解题的进展而扩散，从图7可见，这有3条信息．

　　（a）对顶角相等．　　　　　　　　　　　　④

　　（b）等于第三个量的两个量相等（传递性）． ⑤

　　（c）同位角相等，则两直线平行．　　　　　⑥

　　3）把这两方面的信息（共6条）进行有效的组合，使之成为一个和谐的逻辑结构（共有3步推理）．

　　这样，通过分析解题过程我们看清了，这个题目在解决过程中的知识结构与逻辑关系，进一步还归纳出“什么叫解题”的一个可操作回答：从理解题意中捕捉有用的信息，从记忆储存中提取有关的信息，并将这两组信息组成一个和谐的逻辑结构．

　　6 展开动态想象

　　也许我们一开始就直感到图形表象有一种对称结构（对称美的召唤），它朦朦胧胧只是因为对称中心没有显化．也许是在解题分析中，由于已证明了，所以居中平行线上每一点都是两手行线、的对称中心，而直线上每一点都是直线本身的对称中心，因而图1本身是中心对称图形．

　　于是，我们有这样的直感，图8中若与不平行，必然破坏对称性．这是一种不充分的推理，体现了形象思维的特征，同时也揭示了证明的一个新方向．

　　设上的截点为、，而为线段的中心（图8）．想象会使我们看到，当图形绕点旋转180°时，射线会与射线重合，又由知，射线会与射线重合，从而直线与直线换位，且射线与射线换位．这一想象实际上已经完成了旧表象到新表象的改造，数量关系（保证了旋转180°后图形重合）已经转化为位置关系．否则与在左（右）边有一个交点，则右（左）边也有一个对称的交点，造成和重合，与已知矛盾．