第八节 切线的判定和性质

扩展资料

同一法

　　同一法也是几何中间接证明的方法之一，当一个命题的条件和结论所指的概念唯一存在时，若直接证明有困难，就不妨改为去证它的逆否命题，然后根据唯一性的原理断言命题为真，这种解题方法叫做同一法．

　　用同一法解题一般有三个步骤：

　　（1）先作出一个符合结论的图形，然后推证出所作的图形符合已知条件；

　　（2）根据唯一性，证明所作出的图形与已知的图形是全等的或重合的； 

　　（3）从而说明已知图形符合结论．

　　例1、如图：已知PQ、TR为⊙O的切线，P、R及为切点，PQ∥RT．求证：PR为⊙O的直径．

　　证明：如图，延长PO交RT于R’，

　　　∵PR’⊥PQ，PQ∥RT．

　　　∴PR’⊥RT ，即OR’⊥RT，

　　　连结OR，

　　　∵TR为⊙O的切线，R为切点

　　　∴OR⊥RT，

　　　∴R’与R重合

　　　∴PR为⊙O的直径．

　　例2、已知AB是半圆的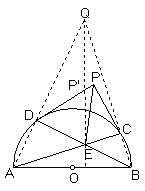直径，过A、B两点分别引弦AC与BD交于E点，又过C、D分别作圆的两条切线交于P，连结PE，求证：PE⊥AB．

　　证明：如图，∵AB是半圆的直径，

　　　∴∠ACB=∠ADB=90°，

　　　延长AD，BC交于Q，那么E为△ABQ的垂心，

　　　连结QE，设QE交DP于P’，显然QE⊥AB．

　　　∵∠PDE=∠DAB=90°-∠DQE=∠DEQ，

　　　∴∠QDP=∠DQE，DP’=P’E=QP’，即DP’平分QE，

　　　同理CP’平分QE，

　　　∵直线DP、CP都经过QR的中点P’，而DP、CP只相交一个点P，

　　　∴P必与QR的中点P’重合．

　　　∵QR⊥AB，∴PE⊥AB．

返回页首