第十四节 两圆的公切线

扩展资料

切点三角形

　　如图，⊙O₁和⊙O₂外切于点A，它们的半径分别为R、r，BC是⊙O₁和⊙O₂的公切线，B，C为切点．连结AB、AC构成的三角形．

　　　△ ABC称为切点三角形．它具有如下性质：

　　（1）△ABC为直角三角形，且∠BAC=90°；

　　（2）若BE、CD分别为⊙O₁和⊙O₂的直径，则E、A、C三点共线，B、A、D三点共线；

　　（3）BC²=4Rr；

　　（4）AB²:AC²=R:r ．（因图形中存在双垂直图形，所以切点三角形还有很多性质）

　　证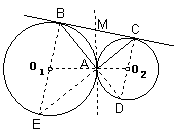明：（1）过点A作⊙O₁和⊙O₂的内切线交BC于点M．

　　∵MA、MB是⊙O₁的切线，

　　∴MA=MB．

　　同理MA=MC．

　　∴ MA=MB=MC．

　　∴∠BAC=90°．

　　（2）由（1）知∠BAC=90°，

　　又∵BE为⊙O₁的直径，∴∠BAE=90°，∴∠BAC+∠BAE=180°

　　∴E、A、C三点共线，同理B、A、D三点也共线．

　　（3）在Rt△BCE和Rt△CDB中，∵∠CBA=∠BEA，∠BCA=∠CDA，

　　∴Rt△BCE∽Rt△CDB，∴BC²=4Rr．

　　（4）Rt△BCE中，∵BA⊥EC，∴ AB² = AE·AC，∴AB²:AC²= AE:AC

　　∵BE∥CD，∴AE:AC= R:r，∴AB²:AC²=R:r ．

　　例、如图，⊙O₁和⊙O₂外切于T，它们的半径之比为3:2，AB是它们的外公切线，A、B是切点，AB＝ ，求⊙O₁和⊙O₂的圆心距．

　　解：连结AT、BT．由条件知△ATB是切点三角形．设⊙O₁和⊙O₂的半径分别为3k、2k．由上述性质，得

　　 ，即 ，k=2，∴O₁O₂=3k+2k=5k=10．

返回页首