第十八节 画正多边形

扩展资料

圆的一种几何等分法

　　在理论上，单使用圆规和直尺，把一个圆周究竟可以准确地分成多少个相等部分?这个问题数学上早已有了完全的解答：并不是可以分成任何数的等分的．

　　可以分成：2，3，4，5，6，8，10，12，15，l6，17，…… 257，……等分．

　　不能分成：7，9，11，13，14，，……等分．

　　更糟糕的是，并没有一个一致的作图方法，比方说，分成15等分的方法和分成12等分的不同，而且，这许多种方法，还不宜记忆．

　　在实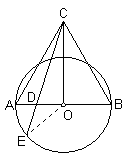际工作中，常常遇到圆的等分问题，需要一种几何的方法求得近似的图形．下面介绍一种有趣的近似的几何方法．

　　假定，要把一个给定的圆周分成九等分．从任一直径AB作一等边三角形ACB，把直径AB在D点分成AD和DB两段，使AD: AB=2:9．(在一般的情形，使AD: AB=2:n)．

　　用线段连接C、D两点，并把它延长到和圆周相交于E点，那时 就大约等于圆周的九分之一(对于一般情， 的度数为 )，即弦AE就等于内接正九边形(或n边形)的一边．这儿可能发生的误差大约是0.8%．

　　假如把方才作图中的圆心角AOE和等分的分数从n的关系表示出来，可得下列公式：

．

的数值很大的时候，上式可以简化成下列近似的公式： ．

　　从另一方面说，把圆周准确地分成n等分，圆心角AOE应该等于 ，把这个数 和AOE角作一比较，可以以得画图中的误差（如下图表）．

n	3	4	5	6	7	8	10	20	60
	120°	90°	72°	60°	51°26'	45°	36°	18°	6°
∠AOE	120°	90°	71°57'	60°	51°31'	45°11'	36°21'	18°38'	6°26'
误差%	0	0	0.7	0	0.17	0.41	0.97	3.5	7.2

　　从上表可知，我们可以用上面这种方法把一个圆周分成5、7、8、10分而不致发生很大的误差，象这样的娱差，在大多数实际情形下，是不碍事的．但是当分成的分数n增加的时候，这个方法的精确性显著降低，就是说误差显著增高；不过在任何n值，这个误差不会超过10％．

返回页首