第四节 简单的线性规划

扩展资料

线性规划的解

　　课本题中出现的线性规划都有唯一的最优解，其实线性规划的解有许多不同的情况，除了有唯一的最优解的情况外，还有

　　（1）无可行解，从而无最优解．这就是约束条件不等式组无解的情况．

　　（2）有无穷多个最优解

　　例2

　　

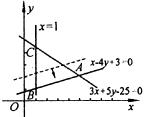
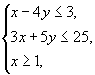
　　我们用图解法求解．

　　由于目标函数等高线和可行域的边界线 平行，沿着目标函数值增加方向平行移动目标函数的等高线，最终停留在直线 上，所以线段AB上的所有点都是最优解．

　　线性规划如果有最优解，只会是有唯一最优解或者有无穷多个最优解这两种情况，不会出现其他情况，这就是下面的命题．

　　命题1  如果线性规划有两个不同的最优解 ，那么对任意 ， 是最优解．

　　这个命题的证明可以在任何一本线性规划的书中找到，这里就不再证明了．事实上证明是平凡的，只要注意到 在线段 上，利用线性性质，读者就可以自己证明．

　　（3）有可行解，无最优解．

　　例3   

　　

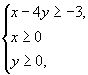
　　我们用图解法求解．

　　从图中可以 看出随着目标函数等高线的移动，目标函数值会越来越大，没有上界．有的书上称之为无界解．

　　无界解的情况只会出现在可行域是开区域的时候．如果可行域是闭区域，就一定是有界的，于是有命题2  如果统性规划可行域是闭区域，那么一定有最优解．

　　只要注意到线性函数是连续函数，上面的命题就是“有界闭区域上连续函数可以达到最大值或最小值”这一定理的一个推理．

　　从上面的例子中我们可以看出，如果有最优解，那么就有可行域的顶点是最优解．所以也可以通过比较可行域顶点的目标函数值来求线性规划的最优解．例如 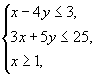， 中的顶点 的目标函数值是 ； 的目标函数值是3； 的目标函数值是 于是通过比较可以知道 是最优解．

　　线性规划的单纯形算法，就是一种从顶点到顶点并使得目标函数值不断改进的迭代算法，由于可行域的顶点只有有限多个，所以经过有限次送代就可以求出线性规划的最优解．单纯形算法可以求解一般的（变量多于两个）线性规划问题．

　　许多实际问题中变量和约束的个数都很多，有些规模比较大的问题中变量和约束的个数甚至可以上万，这样的问题当然是无法用手工计算的，需要用计算机和专门的软件求解．对于规模不是太大（如几十个变量）的线性规划，现在常用的数学软件如Mathematica，Matlab都可以解．下面介绍如何用Matematica解线性规划．

　　用Mathematica解线性规划用的是ConstrainedMax或者 函数，这两个函数的格式如下：

　　 ［目标函数 ， ］

　　 ［目标函数 ， ］

　　由于 软件是用C语言编写的，所以它的函数带有C语言的风格．｛｝表示表格， 和 函数中都有两个表格，第一个表格是约束条件的表，第二个表格是变量表，表格中的项用逗号分隔．要指出的是由于一般的线性规划中的变量都是非负变量，这两个函数的变量也要求有非负约束，但是非负约束可以不在约束条件表格中列出．

　　例如求解线性规划



　　

　　只要输入In［2］：＝ 计算机就会给出计算结果

　　最优值2，最优解： 斜体的 和 自动加上的 表示输入， 表示输出， 中的2表示行号．

　　用 求例l中的规划问题，

　　在许多实际问题中都要求线性规划的最优整数解，课本中也出现了这样的例子和习题．但是笔者以为求最优整数解不应该成为教学的重点．因为求整数解的问题属于整数规划的范畴，而整数规划和线性规划是运筹学中两个不同的分支．教材的作者显然是知道这一点的，所以在教材的处理上回避了如何去求整数解这个问题．作者这样做一方面告诉大家求整数解不应该成为教学的重点，另一方面也给学生留下了一个自由发展的空间．事实上对于课本上出现的这样非常简单的问题只要在非整数优解的附近找出整数可行解，通过比较它们目标函数值的大小就可以求出最优整数解，学生完全可以自己想办法解决．

　　在科普杂志《科学的美国人》（Scientific American）1981年第6期上有一篇介绍线性规划的文章，文章用了下面的一个例子（本文中的数量单位有改动）：

　　某啤酒厂生产两种啤酒，其中淡色啤酒A桶，啤酒B桶．粮食、啤酒花和麦芽是三种有约束的资源，每天分别可以提供480斤、160两和11 90斤．假设生产一桶淡色啤酒需要粮食5斤、啤酒花4两、麦芽20斤；生产一桶啤酒需要粮食15斤、啤酒花4两、麦芽35斤．售出后每桶淡色啤酒可获利13元，每桶啤酒可获利23元．问A，B等于多少时工厂的利润最大．

　　这个例子的线性规划模型是



　　

　　和课本中的例子相比较这个例子有两个优点，一是它的数据更接近实际数据，有真实感，同时由于数字较大求出的最优解不是整数的问题被相对淡化了；另一方面例子中三种约束的单位不同，这在实际问题中经常出现，例子可以告诉学生列规划时并不需要统一各种约束条件的单位．笔者建议在教学中可以使用类似的例子．

选自《中学数学月刊》2002第八期选节